从 AVL 树中删除元素与从 BST 中删除元素相同，只是树可能需要重新平衡。正如从 BST 中删除元素一节中讨论的，要从二叉树中删除元素，算法首先找到包含该元素的节点。让current指向二叉树中包含该元素的节点，parent指向current节点的父节点。 当前节点可以是父节点的左子节点或右子节点。
删除元素时会出现两种情况。

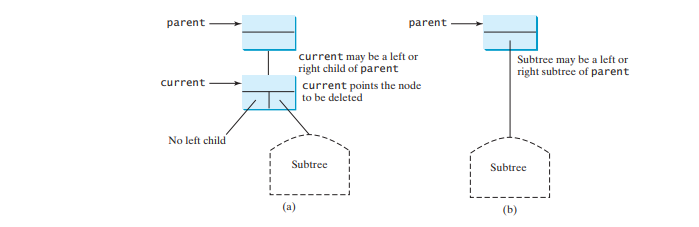
情况一：当前节点没有左子节点，如下图(a)所示。要删除current节点，只需将parent节点与current节点的右子节点连接起来即可，如下图(b)所示。沿从 parent 节点到 root 节点的路径的节点高度可能已减小。为了确保树是平衡的，调用

balancePath(parent.element);

情况2：当前节点有左子节点。设rightMost指向current节点左子树中包含最大元素的节点，parentOfRightMost指向rightMost的父节点节点，如下图(a)所示。 rightMost 节点不能有右子节点，但可以有左子节点。将current节点中的元素值替换为rightMost节点中的元素值，将parentOfRightMost节点与rightMost的左子节点连接起来]节点，删除rightMost节点，如下图(b)所示。

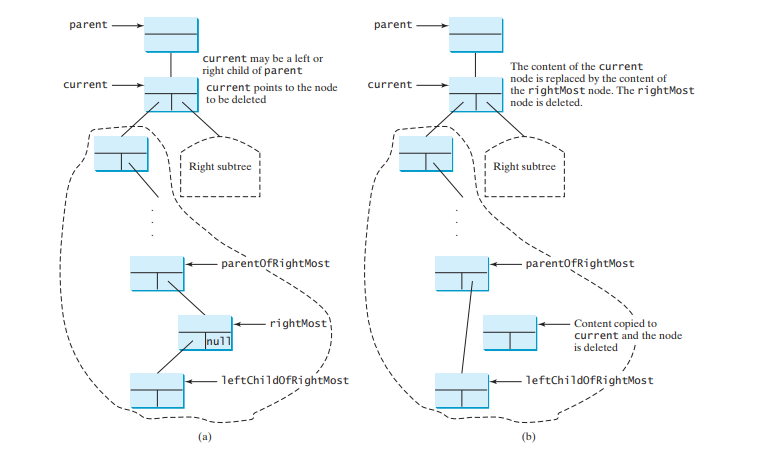
从 parentOfRightMost 到根的路径上的节点高度可能已减小。为了确保树是平衡的，调用

balancePath(parentOfRightMost);