O problema do subarranjo máximo e sua história

No final da década de 1970, o matemático sueco Ulf Grenander discutia um problema: como analisar uma matriz 2D de dados de imagem com mais eficiência do que a força bruta? Os computadores eram lentos e as imagens eram grandes em relação à RAM. Para agravar as coisas, na pior das hipóteses, a força bruta levou tempo O (n ^ 6) (complexidade de tempo sêxtica).

Primeiro, Grenandier simplificou a questão: Dada apenas uma matriz unidimensional de números, como você encontraria de forma mais eficiente a submatriz contígua com a maior soma?

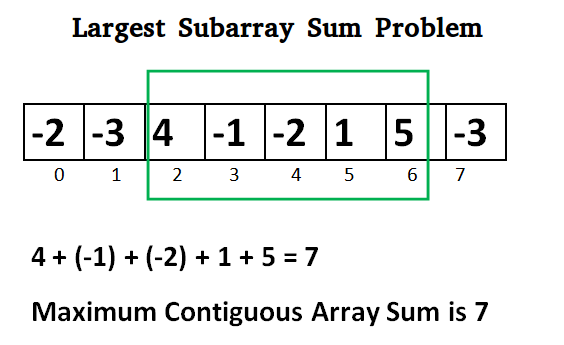
Força bruta: uma abordagem ingênua com complexidade de tempo cúbico

Força bruta, levaria metade do tempo para analisar uma matriz 1D do que uma matriz 2D, então O(n^3) para examinar todas as combinações possíveis (complexidade de tempo cúbico).

def max_subarray_brute_force(arr):
    max_sum = arr[0] # assumes arr has a length

    # iterate over all possible subarrays
    for i in range(len(arr)):
        for j in range(i, len(arr)):
            current_sum = 0
            # sum the elements of the subarray arr[i:j 1]
            for k in range(i, j   1):
                current_sum  = arr[k]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

print(max_subarray_brute_force([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

Otimização O(n²) de Grenander: um passo à frente

Grenander melhorou para solução O(n^2). Não consegui encontrar o código dele em minha pesquisa, mas acho que ele simplesmente se livrou do loop mais interno que soma todos os números entre os dois índices. Em vez disso, podemos manter uma soma acumulada enquanto iteramos no subarray, reduzindo assim o número de loops de três para dois.

def max_subarray_optimized(arr):
    max_sum = arr[0]  # assumes arr has a length

    # iterate over all possible starting points of the subarray
    for i in range(len(arr)):
        current_sum = 0
        # sum the elements of the subarray starting from arr[i]
        for j in range(i, len(arr)):
            current_sum  = arr[j]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

Divisão e conquista de Shamos: dividindo o problema para O (n log n)

Grenander mostrou o problema ao cientista da computação Michael Shamos. Shamos pensou nisso por uma noite e criou um método de dividir e conquistar que é O(n log n).

É muito inteligente. A ideia é dividir o array em duas metades e, em seguida, encontrar recursivamente a soma máxima do subarray para cada metade, bem como o subarray que cruza o ponto médio.

def max_crossing_sum(arr, left, mid, right):
    # left of mid
    left_sum = float('-inf')
    current_sum = 0
    for i in range(mid, left - 1, -1):
        current_sum  = arr[i]
        left_sum = max(left_sum, current_sum)

    # right of mid
    right_sum = float('inf')
    current_sum = 0
    for i in range(mid   1, right   1):
        current_sum  = arr[i]
        right_sum = max(right_sum, current_sum)

    # sum of elements on the left and right of mid, which is the maximum sum that crosses the midpoint
    return left_sum   right_sum

def max_subarray_divide_and_conquer(arr, left, right):
    # base case: only one element
    if left == right:
        return arr[left]

    # find the midpoint
    mid = (left   right) // 2

    # recursively find the maximum subarray sum for the left and right halves
    left_sum = max_subarray_divide_and_conquer(arr, left, mid)
    right_sum = max_subarray_divide_and_conquer(arr, mid   1, right)
    cross_sum = max_crossing_sum(arr, left, mid, right)

    # return the maximum of the three possible cases
    return max(left_sum, right_sum, cross_sum)

def max_subarray(arr):
    return max_subarray_divide_and_conquer(arr, 0, len(arr) - 1)


print(max_subarray([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

Isso reduz a complexidade do tempo para o tempo O (nlogn) porque primeiro a matriz é dividida em duas metades (O (logn)) e, em seguida, encontrar a submatriz de cruzamento máximo leva O (n)

Algoritmo de Kadane: a solução elegante O(n)

O estatístico Jay Kadane analisou o código e imediatamente identificou que a solução de Shamos falhou em usar a restrição de contiguidade como parte da solução.

Aqui está o que ele percebeu

-Se um array tiver apenas números negativos, então a resposta será sempre o maior número do array, assumindo que não estamos permitindo subarrays vazios.

-Se um array tiver apenas números positivos, a resposta será sempre somar o array inteiro.

-Se você tiver uma matriz de números positivos e negativos, poderá percorrer a matriz passo a passo. Se em algum momento o número que você está vendo for maior que a soma de todos os números anteriores, a solução não poderá incluir nenhum dos números anteriores. Assim, você inicia uma nova soma a partir do número atual, enquanto acompanha a soma máxima encontrada até o momento.

maxSubArray(nums):
    # avoiding type errors or index out of bounds errors
    if nums is None or len(nums) == 0:
        return 0


    max_sum = nums[0]  # max sum can't be smaller than any given element
    curr_sum = 0

    # Kadane's algorithm
    for num in nums:
        curr_sum = max(num, curr_sum   num)
        max_sum = max(curr_sum, max_sum)
    return max_sum

O que adoro nesse algoritmo é que ele pode ser aplicado a muitos outros problemas. Tente adaptá-lo para resolver estes problemas do LeetCode:

Unos e Zeros
Submatriz Circular de Soma Máxima
Soma do submatriz de tamanho mínimo
Soma máxima ascendente do submatriz
Submatriz Máxima de Produto
Soma Contínua de Submatriz
Submatriz de soma alternada máxima (premium)
Soma máxima do retângulo não maior que K