Você já se perguntou por que os cassinos sempre parecem ganhar? Em “Vencendo as probabilidades: a matemática por trás dos lucros dos cassinos”, exploraremos a matemática simples e as estratégias inteligentes que garantem que os cassinos ganhem dinheiro no longo prazo. Através de exemplos fáceis de entender e simulações de Monte Carlo, revelaremos os segredos por trás da casa. Prepare-se para descobrir como os cassinos viram as probabilidades a seu favor!

Compreendendo a vantagem da casa

A vantagem da casa é um conceito fundamental no mundo dos cassinos. Representa o lucro médio que o casino espera obter com cada aposta feita pelos jogadores. Essencialmente, é a percentagem de cada aposta que o casino irá reter no longo prazo.

A vantagem da casa existe porque os cassinos não pagam as apostas vencedoras de acordo com as “probabilidades reais” do jogo. As probabilidades verdadeiras representam a probabilidade real de ocorrência de um evento. Ao pagar com probabilidades ligeiramente mais baixas, os casinos garantem lucro ao longo do tempo.

A vantagem da casa (HE) é definida como o lucro do cassino expresso como uma porcentagem da aposta original do jogador.

** Roleta Europeia ** tem apenas um zero verde, totalizando 37 números. Se um jogador apostar $1 no vermelho, ele tem 18/37 de chance de ganhar $1 e 19/37 de perder $1. O valor esperado é:

Valor esperado=( 1 × 18/37 ​) ( −1 × 19/37 ​)= 18/37​ − 19/37​ = −1/37 ​≈ −2,7%

Portanto, na Roleta Europeia a vantagem da casa (HE) está em torno de 2,7%.

Vamos fazer nosso próprio jogo para entendê-lo melhor, um jogo simples de lançamento de dados.

import random

def roll_dice():
    roll = random.randint(1, 100)

    if roll == 100:
        print(roll, 'You rolled a 100 and lost. Better luck next time!')
        return False
    elif roll 

Neste jogo:

• O jogador tem 1/100 de chance de perder se o resultado for 100.

• O jogador tem 50/100 de chance de perder se o lançamento estiver entre 1 e 50.

• O jogador tem 49/100 de chance de ganhar se o resultado estiver entre 51 e 99.

Valor esperado =(1× 49/100​) ( −1× 51/100​) = 49/100​ − 51/100 ​= −2/100 ​ ≈ −2%

Portanto, a vantagem da casa é 2%.

Compreendendo a simulação de Monte Carlo

As simulações de Monte Carlo são uma ferramenta poderosa usada para compreender e prever sistemas complexos, executando inúmeras simulações de um processo e observando os resultados. No contexto dos casinos, as simulações de Monte Carlo podem modelar vários cenários de apostas para mostrar como a vantagem da casa garante rentabilidade a longo prazo. Vamos explorar como funcionam as simulações de Monte Carlo e como elas podem ser aplicadas a um simples jogo de cassino.

O que é uma simulação de Monte Carlo?

Uma simulação de Monte Carlo envolve a geração de variáveis ​​​​aleatórias para simular um processo várias vezes e a análise dos resultados. Ao realizar milhares ou mesmo milhões de iterações, podemos obter uma distribuição de resultados possíveis e obter insights sobre a probabilidade de diferentes eventos.

Aplicando simulação de Monte Carlo ao jogo de lançamento de dados

Usaremos uma simulação de Monte Carlo para modelar o jogo de lançamento de dados que discutimos anteriormente. Isso nos ajudará a entender como a vantagem da casa afeta a lucratividade do jogo ao longo do tempo.

`def monte_carlo_simulation(trials):
    wins = 0
    losses = 0

    for _ in range(trials):
        if roll_dice():
            wins  = 1
        else:
            losses  = 1

    win_percentage = (wins / trials) * 100
    loss_percentage = (losses / trials) * 100
    houseEdge= loss_percentage-win_percentage
    print(f"After {trials} trials:")
    print(f"Win percentage: {win_percentage:.2f}%")
    print(f"Loss percentage: {loss_percentage:.2f}%")
    print(f"House Edge: {houseEdge:.2f}%")

# Run the simulation with 10,000,000 trials
monte_carlo_simulation(10000000)`

Interpretando os resultados

Nesta simulação, executamos o jogo de lançamento de dados 10.000.000 vezes para observar as porcentagens de vitórias e derrotas. Dada a vantagem da casa calculada anteriormente (2%), esperamos que a percentagem de perdas seja ligeiramente superior à percentagem de vitórias.

Depois de executar a simulação, você poderá ver resultados como:

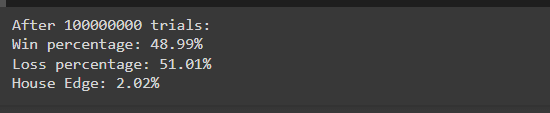
Esses resultados estão intimamente alinhados com as probabilidades teóricas (49% de vitória, 51% de perda), demonstrando como a vantagem da casa se manifesta em um grande número de tentativas. O ligeiro desequilíbrio garante a rentabilidade do casino a longo prazo.

Visualizando vitórias de curto prazo e perdas de longo prazo

As simulações de Monte Carlo são poderosas para modelar e prever resultados por meio de amostragens aleatórias repetidas. No contexto do jogo, podemos usar simulações de Monte Carlo para compreender os resultados potenciais de diferentes estratégias de apostas.

Simularemos um único apostador que faz a mesma aposta inicial em cada rodada e observaremos como o valor de sua conta evolui ao longo de um determinado número de apostas.

Veja como podemos simular e visualizar a jornada de apostas usando Matplotlib:

def bettor_simulation(funds, initial_wager, wager_count):
    value = funds
    wager = initial_wager

    # Lists to store wager count and account value
    wX = []
    vY = []

    current_wager = 1

    while current_wager 



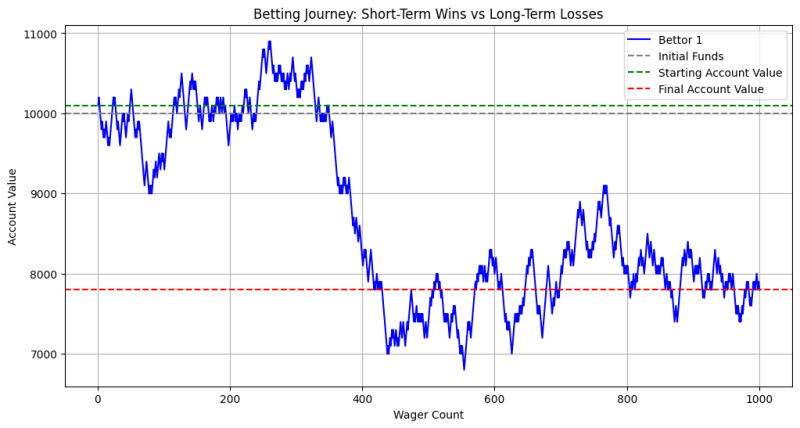
Este gráfico ilustra como o valor da conta de um apostador pode flutuar ao longo do tempo devido a ganhos e perdas. Inicialmente, podem existir períodos de ganhos (linha verde acima do valor inicial), mas à medida que o número de apostas aumenta, o efeito cumulativo da vantagem da casa torna-se evidente. Eventualmente, o valor da conta do apostador tende a diminuir para perto ou abaixo dos fundos iniciais (linha cinzenta), indicando perdas a longo prazo.


  
  
  Conclusão


Compreender a matemática por trás dos lucros do cassino revela uma clara vantagem para a casa em todos os jogos através do conceito de vantagem da casa. Apesar das vitórias ocasionais, a probabilidade incorporada nos jogos de casino garante que a maioria dos jogadores perderá dinheiro ao longo do tempo. As simulações de Monte Carlo ilustram vividamente esta dinâmica, mostrando como mesmo as vitórias a curto prazo podem mascarar perdas a longo prazo devido à vantagem estatística do casino. Esta visão sobre a certeza matemática da rentabilidade do casino sublinha a importância da tomada de decisões informadas e de práticas de jogo responsáveis.

Em seguida, poderíamos explorar visualizações ou variações adicionais, como comparar diferentes estratégias de apostas ou analisar o impacto de diferentes apostas iniciais nos resultados do apostador.

Permaneça conectado:

• GitHub: ezhillragesh

• Twitter: ezhillragesh

• Site: raivash.me

Não hesite em compartilhar suas idéias, fazer perguntas e contribuir para a discussão.

Boa codificação!