Stellen Sie sich vor, wenn Sie nur gerade Linien, Ellipsen und Kreise verwenden könnten, wäre es dann nicht schwierig, ein Auto mit glatten Linien und einem komplexen Erscheinungsbild zu entwerfen?

1962 veröffentlichte der französische Ingenieur Pierre Bézier die Bézier-Kurve, die zunächst für die Karosseriekonstruktion von Autos verwendet wurde.

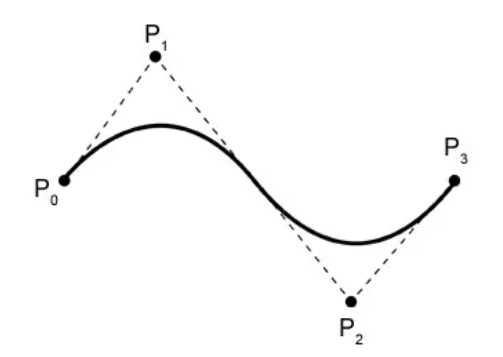
Bézier-Kurven können eine glatte Kurve durch eine Reihe von Kontrollpunkten definieren. Die Kurve verläuft immer durch den ersten und letzten Kontrollpunkt und wird durch die Form der dazwischen liegenden Kontrollpunkte beeinflusst. Darüber hinaus haben Bézier-Kurven die Eigenschaft konvexer Hüllen.

Bézier-Kurven werden häufig in der Computergrafik und Bildmodellierung verwendet, beispielsweise in der Animation, beim Schriftdesign und im Industriedesign.

Formel

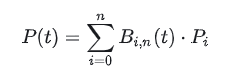
Lassen Sie uns das verstehen.

P(t) stellt einen Punkt auf der Kurve bei t dar (t ist ein Bruch mit einem Wert von 0 bis 1). Was ist ein Punkt auf der Kurve bei t? Eine übliche Kurvenbeschreibung lautet: y = f(x), und zunächst verstehen wir P(t) als f(x). Der Unterschied besteht darin, dass P(t) eine parametrische Darstellung ist (und das Berechnungsergebnis ein „Vektor“ wie [x, y] ist), was später ausführlich erläutert wird.

Als nächstes stellt Pi den i-ten Kontrollpunkt dar (i beginnt bei 0). Am Beispiel der obigen Abbildung gibt es 4 Kontrollpunkte: P0, P1, P2, P3. Das n in der Formel ist der letzte Index der Kontrollpunkte, also n = 3 (beachten Sie, dass es sich nicht um die Anzahl der Kontrollpunkte, sondern um die Anzahl minus 1 handelt).

Bi,n(t) ist die Bernstein-Basisfunktion, auch Basisfunktion genannt. Für jedes spezifische (i, n) gibt es eine andere entsprechende Basisfunktion. Wenn Sie es aus einer gewichteten Perspektive verstehen, können Sie die Basisfunktion als Gewichtsfunktion betrachten, die den „Beitrag“ des i-ten Kontrollpunkts Pi zu den Kurvenkoordinaten an der Position von t angibt.

Die Formel für die Basisfunktion lautet wie folgt:

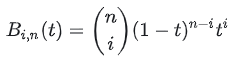
$\left(\genfrac{}{}{0px}{}{n}{i}\right)$( in​) Ist die Kombinationszahl (wie viele Möglichkeiten, i aus n auszuwählen?). Warum die Basisfunktion so aussieht, kann im Zusammenhang mit dem De Casteljau-Algorithmus verstanden werden (siehe später im Text)

Zurück zur P(t)-Formel, ${\sum }_{i=0}^n$∑i=0n ​ ist das Summationssymbol und zeigt an, dass der nachfolgende Teil ( $B_{i,n}(t)\cdot P_i$Bi,n​(t )⋅Pi​ ) soll von i=0 bis i=n summiert werden.

Nehmen Sie die obige Abbildung als Beispiel und gehen Sie davon aus, dass wir P (0,1) berechnen möchten. Wie geht das? Es wird wie folgt erweitert:

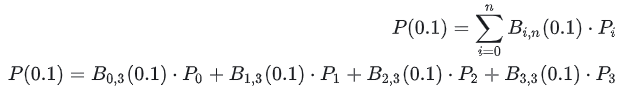
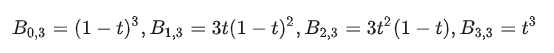
Ersetzen Sie t=0,1, um Folgendes zu erhalten:

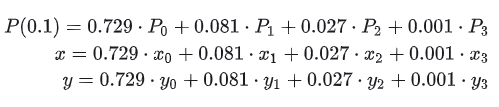
Parametrische Darstellung der Kurve

Hier wird direkt ein Artikel eines Internetnutzers zitiert (Link)

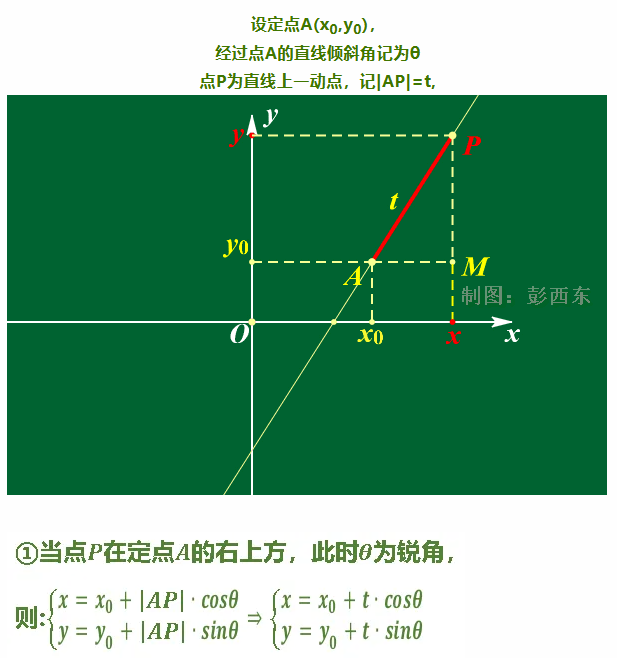
Konzentrieren wir uns auf die obige Formel.

Wie in der obigen Abbildung gezeigt, kann die uns bekannte gerade Linie aus einer anderen Perspektive verstanden werden: Unter Verwendung von t (d. h. der Länge von |AP| vom Punkt P zum bekannten Punkt (x0, y0)) dann kann Punkt P durch die oben genannten trigonometrischen Funktionen bestimmt werden.

Allgemeiner kann es geschrieben werden als:

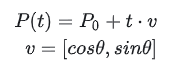
Hier ist P0 der Vektor [x0,y0]und v ist auch ein Vektor. Zusammengenommen ist P(t) der Vektor [x,y].

Ich schaue mir den Kreis noch einmal an:

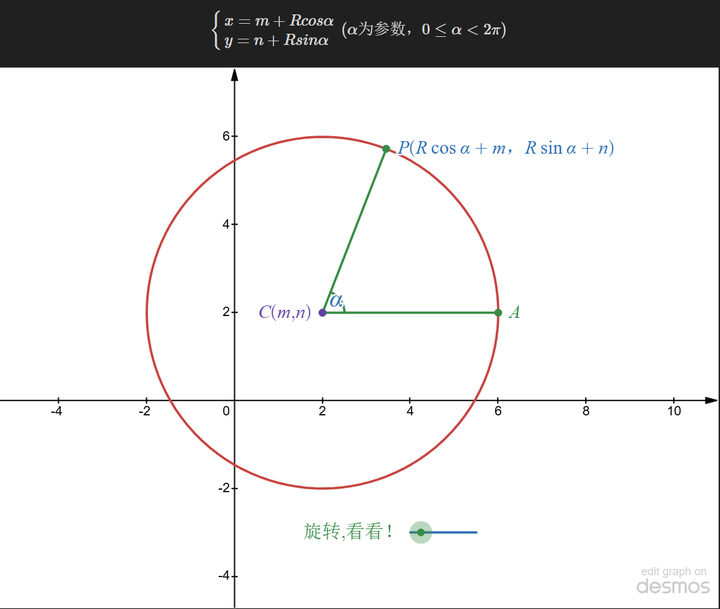
Wie im Diagramm gezeigt, kann der Kreis so betrachtet werden, als hätte er einen bekannten Mittelpunkt, wobei jeder Punkt auf dem Kreis durch den Drehwinkel und den Radius bestimmt wird. Es kann auch geschrieben werden als:

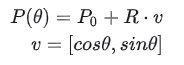
Die parametrischen Gleichungen behalten die geometrische Invarianz bei und können Formen wie Kreise darstellen (wobei ein x mehreren y-Werten entspricht).

De Casteljau

Der De Casteljau-Algorithmus ist eine Methode, die in praktischen Anwendungen verwendet wird, um Bézier-Kurven für Zeichen- und andere Operationen auszuwerten und anzunähern. Im Vergleich zur vorherigen definitionbasierten Bewertungsmethode ist sie schneller und stabiler und näher an den Eigenschaften von Bézier-Kurven.

Hier beziehen wir uns auf zwei Artikel: link1 und link2

Zuerst wird Folgendes definiert:

Sehen Sie sich das obige β an. Es ist etwas verwirrend mit den hochgestellten und tiefgestellten Zeichen; Sie können zum Verständnis die folgende Dreiecksrekursion verwenden:

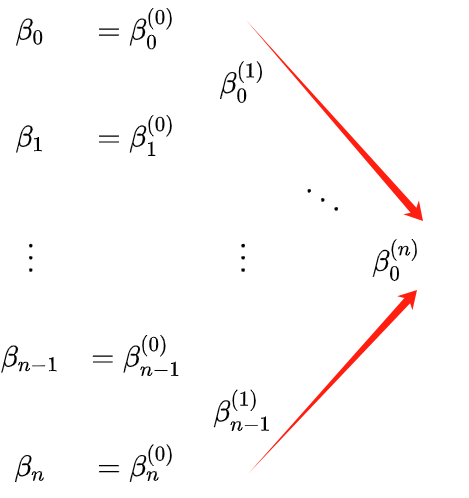
Die roten Kanten des Dreiecks in der obigen Abbildung sind die Kontrollpunkte der beiden Segmente geteilt durch t0. Um t0, P(t0) besser zu verstehen (d. h. ${\beta }_0^{(n)}$β0(n)​ ）, die Kontrollpunkte der beiden Kurven, können Sie sich auf die folgende Abbildung beziehen:

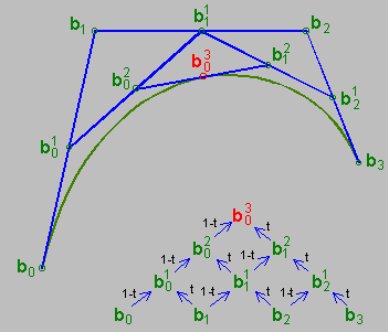
Die obige Abbildung zeigt die Beziehungen zwischen verschiedenen Punkten, wenn t=0,5.

Aus der Perspektive der „Interpolation“ kann der Berechnungsprozess auch als Folgendes verstanden werden:

1. Die Mittelpunkte jedes Paares benachbarter Kontrollpunkte finden (weil t=0,5), also b01, b11, b21 (bitte entschuldigen Sie meine Notation; das Schreiben in LaTeX ist zu mühsam)
2. Finden Sie den Mittelpunkt b02 auf b01−b11 und den Mittelpunkt b12 auf b11-b21
3. Finden Sie den Mittelpunkt b03 auf b02−b12 ​ Tatsächlich ist die Essenz des De Casteljau-Algorithmus Interpolation und Iteration.

Kurvenzeichnung nach De Casteljau

Derzeit werden zwei Methoden beobachtet.

Eine Methode besteht darin, t in kleinen Schritten von 0 auf 1 zu durchlaufen (d. h. 0,01). Jedes Mal, wenn P(t) gesucht wird, wird zur Bestimmung eine rekursive Formel verwendet ${\beta }_0^{(n)}$β0(n)​ .

Die andere Methode beinhaltet die Suche nach P(t=0,5) und dann wird für die beiden geteilten Kurven jeweils P(t=0,5) gesucht... Diese Unterteilung wird fortgesetzt, bis die Kurve angenähert ist.

Durchführung

Es fühlt sich immer unwirklich an, nur zuzuschauen, ohne zu üben.

Also habe ich meinen eigenen Implementierungscode für das Kurvenzeichnen geschrieben und ihn in einem Toolkit organisiert: Compilelife's Toolkit

Der entsprechende Kerncode ist hier