最大子数组问题及其历史

20 世纪 70 年代末，瑞典数学家 Ulf Grenander 一直在讨论一个问题：如何比暴力破解更有效地分析二维图像数据数组？那时的计算机速度很慢，图片相对于 RAM 来说也很大。更糟糕的是，在最坏的情况下，暴力破解需要 O(n^6) 时间（六次时间复杂度）。

首先，Grenandier 简化了问题：给定一个一维数字数组，如何最有效地找到总和最大的连续子数组？

蛮力：一种具有立方时间复杂度的简单方法

蛮力，分析一维数组的时间是分析二维数组的一半，因此检查每种可能的组合（立方时间复杂度）需要 O(n^3)。

def max_subarray_brute_force(arr):
    max_sum = arr[0] # assumes arr has a length

    # iterate over all possible subarrays
    for i in range(len(arr)):
        for j in range(i, len(arr)):
            current_sum = 0
            # sum the elements of the subarray arr[i:j 1]
            for k in range(i, j   1):
                current_sum  = arr[k]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

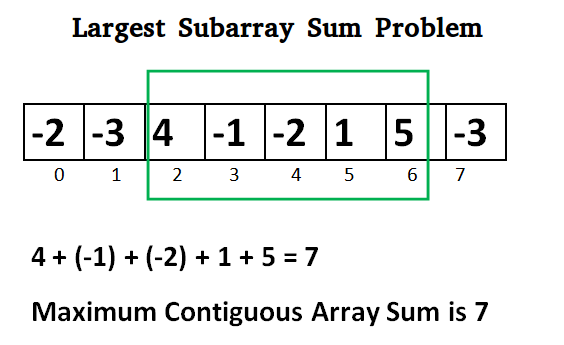
print(max_subarray_brute_force([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

Grenander 的 O(n²) 优化：向前迈出了一步

Grenander 将其改进为 O(n^2) 解决方案。我在研究中找不到他的代码，但我的猜测是他只是摆脱了最内层的循环，该循环将两个索引之间的所有数字相加。相反，我们可以在迭代子数组时保留运行总和，从而将循环次数从三个减少到两个。

def max_subarray_optimized(arr):
    max_sum = arr[0]  # assumes arr has a length

    # iterate over all possible starting points of the subarray
    for i in range(len(arr)):
        current_sum = 0
        # sum the elements of the subarray starting from arr[i]
        for j in range(i, len(arr)):
            current_sum  = arr[j]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

Shamos 的分而治之：将问题分解为 O(n log n)

Grenander 向计算机科学家 Michael Shamos 展示了这个问题。 Shamos想了一个晚上，想出了一个分而治之的方法，O(n log n)。

这很聪明。其思想是将数组分成两半，然后递归地找到每一半的最大子数组和以及穿过中点的子数组。

def max_crossing_sum(arr, left, mid, right):
    # left of mid
    left_sum = float('-inf')
    current_sum = 0
    for i in range(mid, left - 1, -1):
        current_sum  = arr[i]
        left_sum = max(left_sum, current_sum)

    # right of mid
    right_sum = float('inf')
    current_sum = 0
    for i in range(mid   1, right   1):
        current_sum  = arr[i]
        right_sum = max(right_sum, current_sum)

    # sum of elements on the left and right of mid, which is the maximum sum that crosses the midpoint
    return left_sum   right_sum

def max_subarray_divide_and_conquer(arr, left, right):
    # base case: only one element
    if left == right:
        return arr[left]

    # find the midpoint
    mid = (left   right) // 2

    # recursively find the maximum subarray sum for the left and right halves
    left_sum = max_subarray_divide_and_conquer(arr, left, mid)
    right_sum = max_subarray_divide_and_conquer(arr, mid   1, right)
    cross_sum = max_crossing_sum(arr, left, mid, right)

    # return the maximum of the three possible cases
    return max(left_sum, right_sum, cross_sum)

def max_subarray(arr):
    return max_subarray_divide_and_conquer(arr, 0, len(arr) - 1)


print(max_subarray([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

这将时间复杂度降低到 O(nlogn) 时间，因为首先将数组分为两半 (O(logn))，然后找到最大交叉子数组需要 O(n)

Kadane 算法：优雅的 O(n) 解决方案

统计学家 Jay Kadane 查看了代码，立即发现 Shamos 的解决方案未能使用邻接约束作为解决方案的一部分。

这就是他意识到的

-如果数组只有负数，那么答案将始终是数组中最大的数字，假设我们不允许空子数组。

-如果数组只有正数，则答案始终是将整个数组相加。

-如果你有一个同时包含正数和负数的数组，那么你可以逐步遍历该数组。如果在任何时候您正在查看的数字大于其之前的所有数字的总和，则解决方案不能包含任何先前的数字。因此，您从当前数字开始一个新的总和，同时跟踪迄今为止遇到的最大总和。

maxSubArray(nums):
    # avoiding type errors or index out of bounds errors
    if nums is None or len(nums) == 0:
        return 0


    max_sum = nums[0]  # max sum can't be smaller than any given element
    curr_sum = 0

    # Kadane's algorithm
    for num in nums:
        curr_sum = max(num, curr_sum   num)
        max_sum = max(curr_sum, max_sum)
    return max_sum

我喜欢这个算法的原因是它可以应用于许多其他问题。尝试调整它来解决这些 LeetCode 问题：

个和零
循环子数组的最大和
最小大小子数组和
最大升序子数组和
最大乘积子数组
连续子数组和
最大交替和子数组（高级）
矩形的最大和不大于 K