Entropix：最大化推理效能的取樣技術

根據 Entropix README，Entropix 使用基於熵的取樣方法。本文講解了基於熵和變熵的具體採樣技術。

熵和變熵

讓我們先解釋熵和變熵，因為它們是確定採樣策略的關鍵因素。

熵

在資訊理論中，熵是隨機變數不確定性的量測。隨機變數 X 的熵由下列方程式定義：

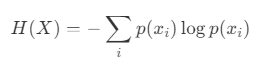
• X：離散隨機變數。
• x_i：X的第i種可能狀態。
• p(x_i)：狀態x_i的機率。

當機率分佈均勻時，熵最大化。相反，當特定狀態比其他狀態更有可能出現時，熵就會減少。

變熵

變熵與熵密切相關，代表資訊內容的可變性。考慮隨機變數 X 的資訊內容 I(X)、熵 H(X) 和方差，變熵 V E(X) 定義如下：

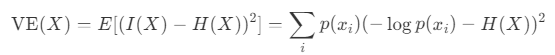
當機率 p(x_i) 變化很大時，變熵變大。當機率均勻時（無論是當分佈具有最大熵時，還是當一個值的機率為 1 而所有其他值的機率為 0 時），它會變小。

抽樣方法

接下來，讓我們探討採樣策略如何根據熵和變熵值變化。

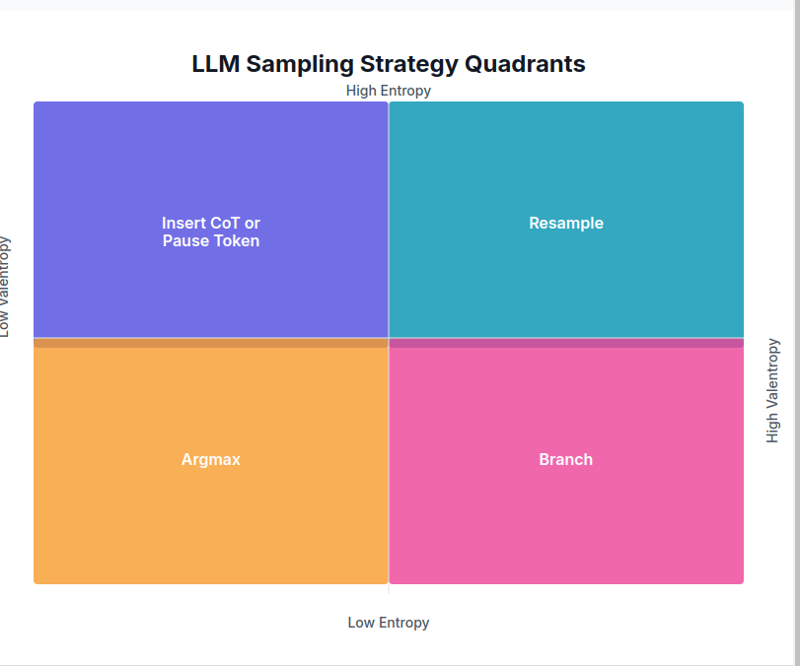
1. 低熵、低變熵 → Argmax

在這種情況下，特定令牌的預測機率比其他代幣高得多。由於下一個標記幾乎確定，因此使用 Argmax。

if ent 



代碼連結


  
  
  2. 低熵、高變熵 → 分支


當有一定的信心，但存在多種可行的選擇時，就會發生這種情況。在這種情況下，分支策略用於從多個選擇中進行取樣並選擇最佳結果。 


elif ent  5.0:
    temp_adj = 1.2   0.3 * interaction_strength
    top_k_adj = max(5, int(top_k * (1   0.5 * (1 - agreement))))
    return _sample(logits, temperature=min(1.5, temperature * temp_adj), top_p=top_p, top_k=top_k_adj, min_p=min_p, generator=generator)




代碼連結

雖然這種策略被稱為“分支”，但目前的程式碼似乎是調整取樣範圍並選擇單一路徑。 （如果有人有更多見解，我們將不勝感激。）


  
  
  3. 高熵、低變熵 → CoT 或插入暫停令牌


當下一個token的預測機率相當均勻時，表示下一個上下文不確定，則插入一個澄清token來解決歧義。 


elif ent > 3.0 and vent 



代碼連結


  
  
  4. 高熵、高變熵 → 重採樣


在這種情況下，存在多個上下文，且下一個標記的預測機率較低。 重採樣策略採用較高的溫度設定和較低的 top-p。 


elif ent > 5.0 and vent > 5.0:
    temp_adj = 2.0   0.5 * attn_vent
    top_p_adj = max(0.5, top_p - 0.2 * attn_ent)
    return _sample(logits, temperature=max(2.0, temperature * temp_adj), top_p=top_p_adj, top_k=top_k, min_p=min_p, generator=generator)




代碼連結


  
  
  中級案例


如果上述條件都不滿足，則執行自適應採樣。採取多個樣本，根據熵、變熵和注意力資訊計算最佳採樣分數。 


else:
    return adaptive_sample(
        logits,
        metrics,
        gen_tokens,
        n_samples=5,
        base_temp=temperature,
        base_top_p=top_p,
        base_top_k=top_k,
        generator=generator
    )




代碼連結



  
  
  參考

• Entropix 儲存庫
• Entropix 在做什麼？