Взвешенную задачу девяти хвостов можно свести к взвешенной задаче о кратчайшем пути.
В разделе была представлена ​​задача девяти хвостов и решена ее с помощью алгоритма BFS. В этом разделе представлен вариант проблемы и решена ее с использованием алгоритма кратчайшего пути.

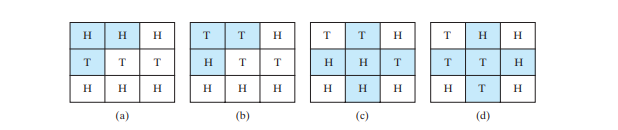
Задача девяти решок состоит в том, чтобы найти минимальное количество ходов, при которых все монеты будут лежать лицом вниз. Каждый ход переворачивает монету-голову и ее соседей. В задаче о взвешенных девяти решках количество бросков назначается в качестве веса каждому ходу. Например, вы можете заменить монеты на рисунке ниже a на монеты на рисунке ниже b, перевернув первую монету в первом ряду и две ее соседи. Таким образом, вес этого хода равен 3. Вы можете заменить монеты с рисунка ниже c на рисунок ниже d, перевернув центральную монету и четырех ее соседей. Таким образом, вес этого хода равен 5.

Задачу девяти хвостов с взвешиванием можно свести к поиску кратчайшего пути от начального узла к целевому узлу во взвешенном по ребрам графе. Граф имеет 512 узлов. Создайте ребро от узла v до u, если есть переход от узла u к узлу v. Назначьте количество переворотов как вес ребра.

Напомним, что в разделе мы определили класс NineTailModel для моделирования задачи девяти хвостов. Теперь мы определяем новый класс с именем WeightedNineTailModel, который расширяет NineTailModel, как показано на рисунке ниже.

Класс NineTailModel создает граф и получает дерево с корнем в целевом узле 511. WeightedNineTailModel аналогичен NineTailModel за исключением того, что он создает WeightedGraph и получает ShortestPathTree с корнем в целевом узле 511. WeightedNineTailModel расширяет NineTailModel. Метод getEdges() находит все ребра в графе. Метод getNumberOfFlips(int u, int v) возвращает количество переворотов от узла u к узлу v. Метод getNumberOfFlips(int u) возвращает количество переворотов от узла u до целевого узла.

Приведенный ниже код реализует WeightedNineTailModel.

package demo;
import java.util.*;

public class WeightedNineTailModel extends NineTailModel {
    /** Construct a model */
    public WeightedNineTailModel() {
        // Create edges
        List edges = getEdges();

        // Create a graph
        WeightedGraph graph = new WeightedGraph(edges, NUMBER_OF_NODES);

        // Obtain a shortest path tree rooted at the target node
        tree = graph.getShortestPath(511);
    }

    /** Create all edges for the graph */
    private List getEdges() {
        // Store edges
        List edges = new ArrayList();

        for(int u = 0; u .ShortestPathTree)tree).getCost(u);
    }
}

WeightedNineTailModel расширяет NineTailModel для построения WeightedGraph для моделирования взвешенной задачи девяти хвостов (строки 10–11). Для каждого узла u метод getEdges() находит перевернутый узел v и назначает количество переворотов в качестве веса ребра (v, u) (строка 30). Метод getNumberOfFlips(int u, int v) возвращает количество переворотов от узла u к узлу v (строки 38–47). Количество переворотов — это количество различных ячеек между
два узла (строка 44).

WeightedNineTailModel получает ShortestPathTree с корнем в целевом узле 511 (строка 14). Обратите внимание, что tree — это защищенное поле данных, определенное в NineTailModel, а ShortestPathTree — это подкласс Tree. Методы, определенные в NineTailModel, используют свойство tree.

Метод getNumberOfFlips(int u) (строки 49–52) возвращает количество переворотов от узла u до целевого узла, которое является стоимостью пути от узла u к целевому узлу. Эту стоимость можно получить, вызвав метод getCost(u), определенный в классе ShortestPathTree (строка 51).

Приведенный ниже код представляет собой программу, которая предлагает пользователю ввести начальный узел и отображает минимальное количество переворотов для достижения целевого узла.

package demo;

import java.util.Scanner;

public class WeightedNineTail {

    public static void main(String[] args) {
        // Prompt the user to enter nine coins' Hs and Ts
        System.out.print("Enter the initial nine coins Hs and Ts: ");
        Scanner input = new Scanner(System.in);
        String s = input.nextLine();
        char[] initialNode = s.toCharArray();

        WeightedNineTailModel model = new WeightedNineTailModel();
        java.util.List path = model.getShortestPath(NineTailModel.getIndex(initialNode));

        System.out.println("The steps to flip the coins are ");
        for (int i = 0; i 



Введите первые девять монет Hs и Ts: HHHTTTTHHH

Чтобы подбросить монеты, выполните следующие действия:

ЧЧХ

ТТТ

ХХХ

ЧЧХ

ЭТО

ТТТ

ТТТ

ТТТ

ТТТ

Количество переворотов — 8

Программа предлагает пользователю ввести начальный узел из девяти букв с комбинацией Hs и Ts в виде строки в строке 8, получает массив символов из строка (строка 9), создает модель (строка 11), получает кратчайший путь от начального узла до целевого узла (строки 12–13), отображает узлы пути (строки 16–17) и вызывает getNumberOfFlips для получения количества переворотов, необходимых для достижения целевого узла (строка 20).