Представьте, если бы вы могли использовать только прямые линии, эллипсы и круги, не было бы сложно спроектировать автомобиль с плавными линиями и сложным внешним видом?

В 1962 году французский инженер Пьер Безье опубликовал кривую Безье, которая первоначально использовалась для конструкции кузова автомобилей.

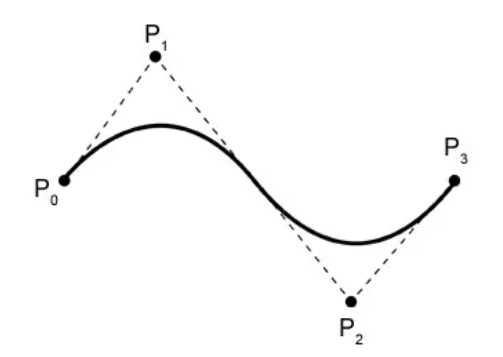
Кривые Безье могут определять плавную кривую через ряд контрольных точек. Кривая всегда проходит через первую и последнюю контрольные точки, и на нее влияет форма промежуточных контрольных точек. Кроме того, кривые Безье обладают свойством выпуклой оболочки.

Кривые Безье широко используются в компьютерной графике и моделировании изображений, например, в анимации, дизайне шрифтов и промышленном дизайне.

Формула

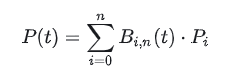
Давайте разберемся в этом.

P(t) представляет точку на кривой в момент t (t — дробь со значением от 0 до 1). Что такое точка на кривой в точке t? Обычное описание кривой таково: y = f(x), а сейчас давайте понимать P(t) как f(x). Разница в том, что P(t) — это параметрическое представление (а результатом вычисления является «вектор», например [x, y]), что будет подробно объяснено позже.

Далее Pi представляет i-ю контрольную точку (i начинается с 0). Если взять приведенный выше рисунок в качестве примера, то имеется 4 контрольные точки: P0, P1, P2, P3. n в формуле — это последний индекс контрольных точек, то есть n = 3 (обратите внимание, что это не количество контрольных точек, а количество минус 1).

Bi,n(t) — базисная функция Бернштейна, также известная как базисная функция. Каждому конкретному (i, n) соответствует своя базисная функция. Если вы понимаете с взвешенной точки зрения, вы можете рассматривать базисную функцию как весовую функцию, указывающую «вклад» i-й контрольной точки Pi в координаты кривой в позиции t.

Формула базисной функции выглядит следующим образом:

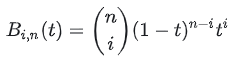
$\left(\genfrac{}{}{0px}{}{n}{i}\right)$( in​) Является числом комбинации (сколько способов выбрать i из n?). Что касается того, почему базисная функция выглядит именно так, то это можно понять в связи с алгоритмом Де Кастельжо (см. далее по тексту)

Вернемся к формуле P(t), ${\sum }_{i=0}^n$∑i=0n ​ — символ суммирования, указывающий, что последующая часть ( $B_{i,n}(t)\cdot P_i$Bi,n​(t )⋅Pi​ ) суммируется от i=0 до i=n.

Возьмем приведенный выше рисунок в качестве примера и предположим, что мы хотим вычислить P(0,1), как это сделать? Он расширяется следующим образом:

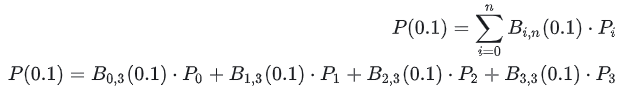
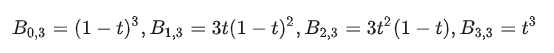
Замените t=0.1, чтобы получить:

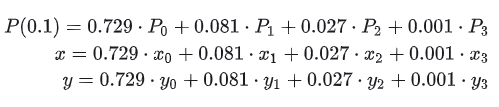
Параметрическое представление кривой

Здесь непосредственно цитируется статья пользователя сети (ссылка)

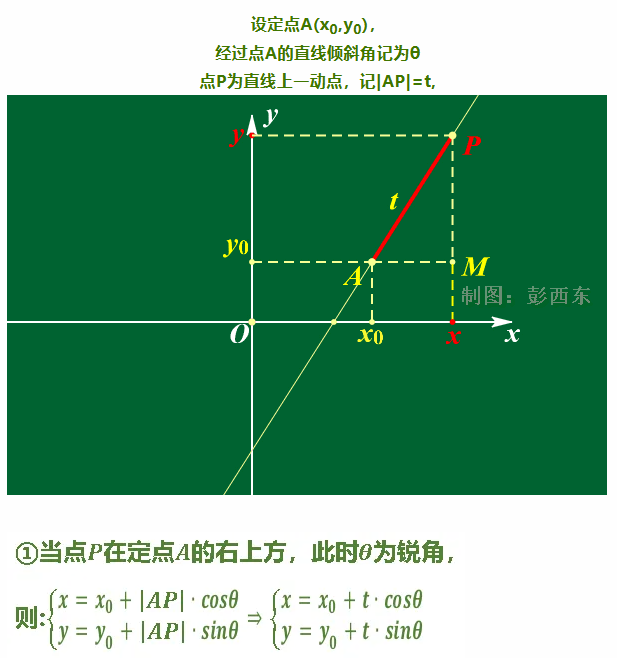
Давайте сосредоточимся на приведенной выше формуле.

Как показано на рисунке выше, знакомую нам прямую линию можно понять и с другой точки зрения: используя t (т.е. длину |AP| от точки P до известной точки (x0,y0)), тогда точку P можно определить с помощью приведенных выше тригонометрических функций.

В более общем смысле это можно записать так:

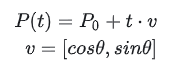
Здесь P0 — вектор [x0,y0], а v — тоже вектор. В сумме P(t) представляет собой вектор [x,y].

Снова смотрю на круг:

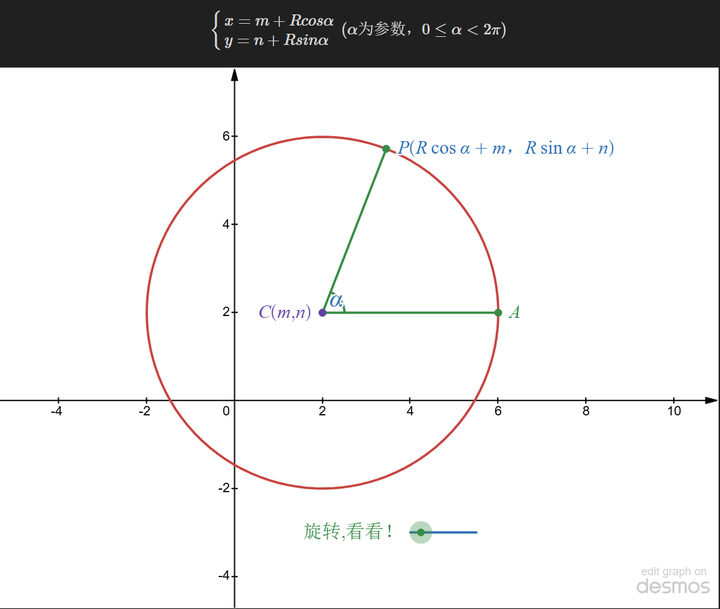
Как показано на диаграмме, круг можно рассматривать как имеющий известный центр, при этом любая точка круга определяется углом поворота и радиусом. Это также можно записать как:

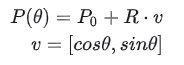
Параметрические уравнения сохраняют геометрическую инвариантность и могут представлять собой фигуры, подобные кругам (где одному x соответствует несколько значений y).

Де Кастельжау

Алгоритм Де Кастельжо — это метод, используемый в практических приложениях для оценки и аппроксимации кривых Безье для рисования и других операций. По сравнению с предыдущим методом оценки, основанным на определениях, он быстрее и стабильнее и ближе к характеристикам кривых Безье.

Здесь мы имеем в виду две статьи: ссылка1 и ссылка2

Во-первых, определяется следующее:

Посмотрите на приведенное выше значение β. Немного сбивают с толку верхние и нижние индексы; для понимания вы можете использовать следующую треугольную рекурсию:

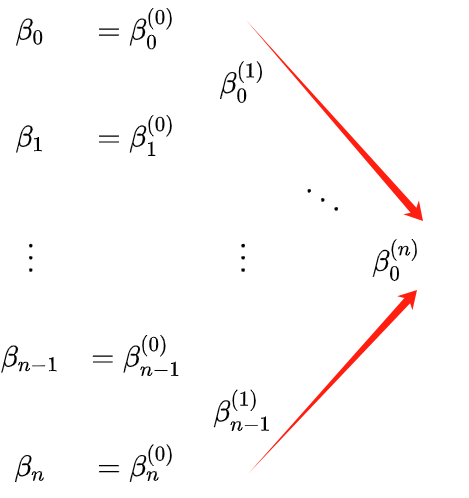
Красные края треугольника на рисунке выше — это контрольные точки двух сегментов, разделенных на t0. Чтобы более наглядно понять t0, P(t0) （т.е. ${\beta }_0^{(n)}$β0(n)​ ）, контрольные точки двух кривых, вы можете посмотреть на следующем рисунке:

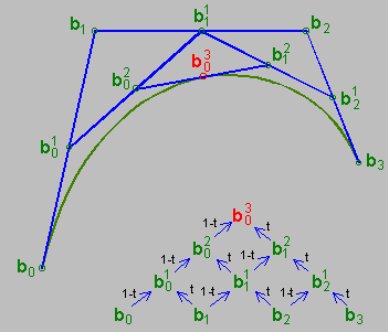
На рисунке выше показаны взаимосвязи между различными точками при t=0,5.

С точки зрения «интерполяции» процесс расчета также можно понимать как:

1. Нахождение середин каждой пары соседних контрольных точек (потому что t=0,5), то есть b01, b11, b21 (простите за мои обозначения, писать в LaTeX слишком хлопотно)
2. Найдите среднюю точку b02 на b01-b11 и найдите среднюю точку b12 на b11-b21
3. Найдите среднюю точку b03 на b02−b12. ​ По сути, суть алгоритма Де Кастельжо — это интерполяция и итерация.

Рисование кривой на основе Де Кастельжо

В настоящее время наблюдаются два метода.

Один метод включает в себя перемещение t от 0 до 1 с небольшим шагом (т.е. 0,01). Каждый раз, когда ищется P(t), используется рекурсивная формула для определения ${\beta }_0^{(n)}$β0(n)​ .

Другой метод включает поиск P(t=0,5), а затем для двух разделенных кривых ищется P(t=0,5) соответственно... Это подразделение продолжается до тех пор, пока кривая не будет аппроксимирована.

Выполнение

Всегда кажется нереальным просто смотреть, не тренируясь.

Поэтому я написал свой собственный код реализации для рисования кривых и организовал его в набор инструментов: Compilelife's Toolkit

Соответствующий основной код находится здесь