k-регрессия ближайших соседей

Регрессия k-ближайших соседей (k-NN) — это непараметрический метод, который прогнозирует выходное значение на основе среднего (или средневзвешенного) k-ближайших точек обучающих данных в пространстве признаков. Этот подход позволяет эффективно моделировать сложные отношения в данных, не принимая при этом конкретную функциональную форму.

Метод регрессии k-NN можно резюмировать следующим образом:

1. Метрика расстояния: алгоритм использует метрику расстояния (обычно евклидово расстояние) для определения «близости» точек данных.
2. k Neighbours: параметр k указывает, сколько ближайших соседей следует учитывать при составлении прогнозов.
3. Прогноз: прогнозируемое значение для новой точки данных представляет собой среднее значение k ее ближайших соседей.

Ключевые понятия

1. Непараметрический: В отличие от параметрических моделей, k-NN не принимает определенную форму для базовой взаимосвязи между входными признаками и целевой переменной. Это делает его гибким при захвате сложных шаблонов.

2. Расчет расстояния: выбор метрики расстояния может существенно повлиять на производительность модели. Общие метрики включают расстояния Евклида, Манхэттена и Минковского.

3. Выбор k: количество соседей (k) может быть выбрано на основе перекрестной проверки. Маленькое k может привести к переобучению, тогда как большое k может слишком сильно сгладить прогноз, что может привести к недостаточному подгонке.

Пример регрессии k-ближайших соседей

В этом примере показано, как использовать регрессию k-NN с полиномиальными характеристиками для моделирования сложных отношений, используя при этом непараметрическую природу k-NN.

Пример кода Python

1. Импортировать библиотеки

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, r2_score

Этот блок импортирует необходимые библиотеки для манипулирования данными, построения графиков и машинного обучения.

2. Создать образец данных

np.random.seed(42)  # For reproducibility
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = 3 * X.ravel()   np.sin(2 * X.ravel()) * 5   np.random.normal(0, 1, 100)

Этот блок генерирует выборочные данные, представляющие взаимосвязь с некоторым шумом, имитируя изменения реальных данных.

3. Разделить набор данных

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Этот блок разбивает набор данных на обучающий и тестовый наборы для оценки модели.

4. Создать полиномиальные объекты

degree = 3  # Change this value for different polynomial degrees
poly = PolynomialFeatures(degree=degree)
X_poly_train = poly.fit_transform(X_train)
X_poly_test = poly.transform(X_test)

Этот блок генерирует полиномиальные функции из наборов обучающих и тестовых данных, позволяя модели фиксировать нелинейные зависимости.

5. Создайте и обучите регрессионную модель k-NN

k = 5  # Number of neighbors
knn_model = KNeighborsRegressor(n_neighbors=k)
knn_model.fit(X_poly_train, y_train)

Этот блок инициализирует регрессионную модель k-NN и обучает ее с использованием полиномиальных функций, полученных из набора обучающих данных.

6. Делайте прогнозы

y_pred = knn_model.predict(X_poly_test)

Этот блок использует обученную модель для прогнозирования на тестовом наборе.

7. Постройте график результатов

plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', alpha=0.5, label='Data Points')
X_grid = np.linspace(0, 10, 1000).reshape(-1, 1)
X_poly_grid = poly.transform(X_grid)
y_grid = knn_model.predict(X_poly_grid)
plt.plot(X_grid, y_grid, color='red', linewidth=2, label=f'k-NN Regression (k={k}, Degree {degree})')
plt.title(f'k-NN Regression (Polynomial Degree {degree})')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()

Этот блок создает диаграмму рассеяния фактических точек данных в сравнении с прогнозируемыми значениями из модели регрессии k-NN, визуализируя подобранную кривую.

Вывод с k = 1:

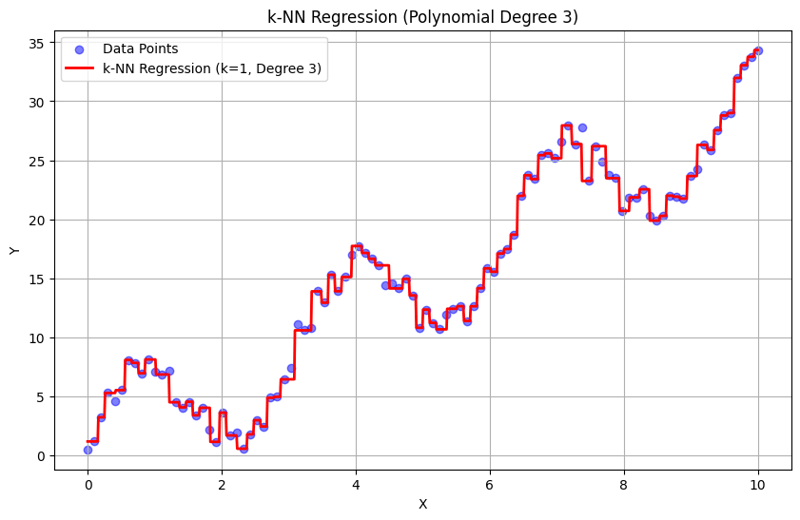
Вывод с k = 10:

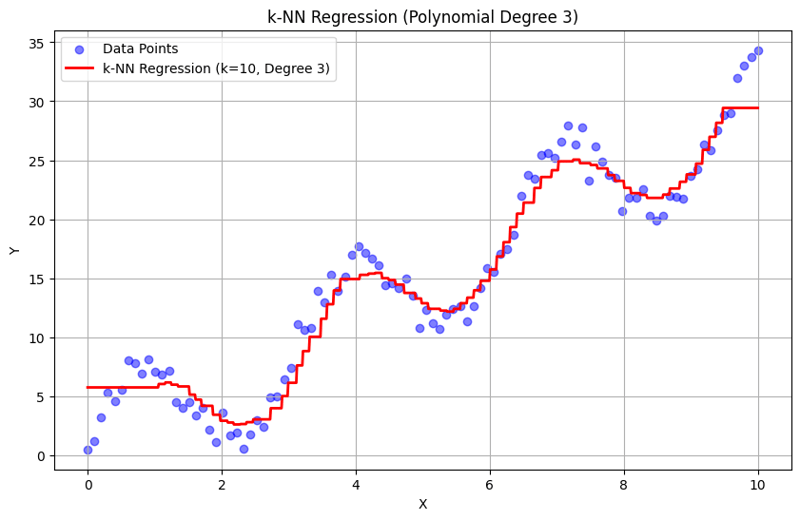
Этот структурированный подход демонстрирует, как реализовать и оценить регрессию k-ближайших соседей с полиномиальными функциями. Улавливая локальные закономерности путем усреднения ответов ближайших соседей, регрессия k-NN эффективно моделирует сложные взаимосвязи в данных, обеспечивая при этом простую реализацию. Выбор k и степени полинома существенно влияет на производительность модели и ее гибкость в выявлении основных тенденций.