Проблема максимального подмассива и ее история

В конце 1970-х годов шведский математик Ульф Гренандер обсуждал проблему: как можно анализировать двумерный массив данных изображений более эффективно, чем грубая сила? Компьютеры тогда были медленными, а изображения были большими по сравнению с оперативной памятью. Ситуация усугублялась тем, что в худшем случае грубая сила занимала время O(n^6) (секстическая временная сложность).

Во-первых, Гренандье упростил вопрос: имея только одномерный массив чисел, как наиболее эффективно найти непрерывный подмассив с наибольшей суммой?

Грубая сила: наивный подход с кубической временной сложностью

Грубая сила, анализ 1D-массива занял бы вдвое меньше времени, чем 2D-массива, поэтому O(n^3) для проверки каждой возможной комбинации (кубическая временная сложность).

def max_subarray_brute_force(arr):
    max_sum = arr[0] # assumes arr has a length

    # iterate over all possible subarrays
    for i in range(len(arr)):
        for j in range(i, len(arr)):
            current_sum = 0
            # sum the elements of the subarray arr[i:j 1]
            for k in range(i, j   1):
                current_sum  = arr[k]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

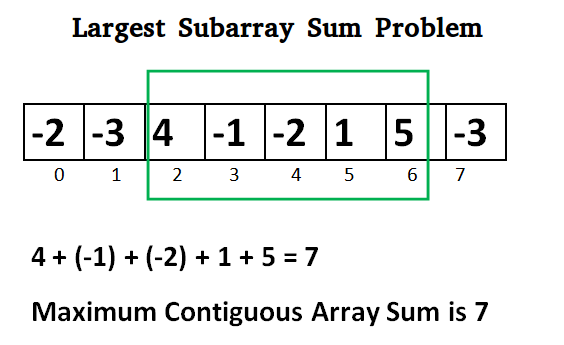
print(max_subarray_brute_force([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

Оптимизация Гренандера O(n²): шаг вперед

Гренандер улучшил его до решения O(n^2). Я не смог найти его код в своих исследованиях, но я предполагаю, что он просто избавился от самого внутреннего цикла, который суммирует все числа между двумя индексами. Вместо этого мы можем сохранять текущую сумму при переборе подмассива, тем самым уменьшая количество циклов с трех до двух.

def max_subarray_optimized(arr):
    max_sum = arr[0]  # assumes arr has a length

    # iterate over all possible starting points of the subarray
    for i in range(len(arr)):
        current_sum = 0
        # sum the elements of the subarray starting from arr[i]
        for j in range(i, len(arr)):
            current_sum  = arr[j]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

Разделяй и властвуй Шамоса: разделение проблемы для O (n log n)

Гренандер показал проблему учёному-компьютерщику Майклу Шамосу. Шамос думал об этом одну ночь и придумал метод «разделяй и властвуй», который представляет собой O(n log n).

Это довольно умно. Идея состоит в том, чтобы разделить массив на две половины, а затем рекурсивно найти максимальную сумму подмассива для каждой половины, а также подмассив, пересекающий среднюю точку.

def max_crossing_sum(arr, left, mid, right):
    # left of mid
    left_sum = float('-inf')
    current_sum = 0
    for i in range(mid, left - 1, -1):
        current_sum  = arr[i]
        left_sum = max(left_sum, current_sum)

    # right of mid
    right_sum = float('inf')
    current_sum = 0
    for i in range(mid   1, right   1):
        current_sum  = arr[i]
        right_sum = max(right_sum, current_sum)

    # sum of elements on the left and right of mid, which is the maximum sum that crosses the midpoint
    return left_sum   right_sum

def max_subarray_divide_and_conquer(arr, left, right):
    # base case: only one element
    if left == right:
        return arr[left]

    # find the midpoint
    mid = (left   right) // 2

    # recursively find the maximum subarray sum for the left and right halves
    left_sum = max_subarray_divide_and_conquer(arr, left, mid)
    right_sum = max_subarray_divide_and_conquer(arr, mid   1, right)
    cross_sum = max_crossing_sum(arr, left, mid, right)

    # return the maximum of the three possible cases
    return max(left_sum, right_sum, cross_sum)

def max_subarray(arr):
    return max_subarray_divide_and_conquer(arr, 0, len(arr) - 1)


print(max_subarray([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

Это уменьшает временную сложность до времени O(nlogn), поскольку сначала массив делится на две половины (O(logn)) и затем поиск подмассива с максимальным пересечением занимает O(n)

Алгоритм Кадане: элегантное решение O(n)

Стастик Джей Кадане просмотрел код и сразу определил, что в решении Шамоса не удалось использовать ограничение непрерывности как часть решения.

Вот что он понял

 — Если массив содержит только отрицательные числа, то ответом всегда будет единственное наибольшее число в массиве, при условии, что мы не допускаем пустых подмассивов.

-Если массив содержит только положительные числа, ответом всегда будет сложение всего массива.

-Если у вас есть массив как положительных, так и отрицательных чисел, вы можете перемещаться по массиву шаг за шагом. Если в какой-то момент число, на которое вы смотрите, больше суммы всех чисел, которые были до него, решение не может включать ни одно из предыдущих чисел. Таким образом, вы начинаете новую сумму с текущего числа, отслеживая при этом максимальную сумму, обнаруженную на данный момент.

maxSubArray(nums):
    # avoiding type errors or index out of bounds errors
    if nums is None or len(nums) == 0:
        return 0


    max_sum = nums[0]  # max sum can't be smaller than any given element
    curr_sum = 0

    # Kadane's algorithm
    for num in nums:
        curr_sum = max(num, curr_sum   num)
        max_sum = max(curr_sum, max_sum)
    return max_sum

Что мне нравится в этом алгоритме, так это то, что его можно применить ко множеству других задач. Попробуйте адаптировать его для решения следующих проблем с LeetCode:

Единицы и нули
Круговой подмассив максимальной суммы
Сумма подмассива минимального размера
Максимальная сумма возрастающего подмассива
Максимальный подмассив продуктов
Непрерывная сумма подмассивов
Подмассив максимальной чередующейся суммы (премиум)
Максимальная сумма прямоугольника не больше K