O problema ponderado das nove caudas pode ser reduzido ao problema do caminho mais curto ponderado.
A seção apresentou o problema das nove caudas e o resolveu usando o algoritmo BFS. Esta seção apresenta uma variação do problema e o resolve usando o algoritmo do caminho mais curto.

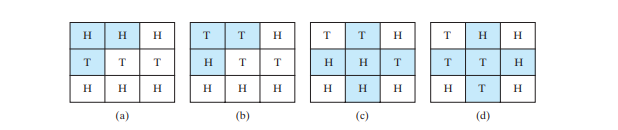
O problema das nove caudas é encontrar o número mínimo de movimentos que levam todas as moedas para baixo. Cada movimento lança uma moeda cara e seus vizinhos. O problema das nove caudas ponderadas atribui o número de lançamentos como um peso em cada movimento. Por exemplo, você pode trocar as moedas da Figura abaixo a pelas da Figura abaixo b jogando a primeira moeda da primeira linha e suas duas vizinhas. Assim, o peso para este movimento é 3. Você pode alterar as moedas da Figura abaixo de c para a Figura abaixo de d jogando a moeda central e suas quatro vizinhas. Portanto, o peso para esse movimento é 5.

O problema das nove caudas ponderadas pode ser reduzido a encontrar o caminho mais curto de um nó inicial até o nó alvo em um gráfico ponderado por arestas. O gráfico possui 512 nós. Crie uma aresta do nó v para u se houver uma mudança do nó u para o nó v. Atribua o número de lançamentos ao peso da aresta.

Lembre-se de que na Seção definimos uma classe NineTailModel para modelar o problema das nove caudas. Agora definimos uma nova classe chamada WeightedNineTailModel que estende NineTailModel, conforme mostrado na figura abaixo.

A classe NineTailModel cria um Graph e obtém uma Tree enraizada no nó de destino 511. WeightedNineTailModel é o mesmo que NineTailModel, exceto que ele cria um WeightedGraph e obtém um ShortestPathTree enraizado no nó de destino 511. WeightedNineTailModel estende NineTailModel. O método getEdges() encontra todas as arestas do gráfico. O método getNumberOfFlips(int u, int v) retorna o número de inversões do nó u para o nó v. O método getNumberOfFlips(int u) retorna o número de inversões do nó u para o nó de destino.

O código abaixo implementa WeightedNineTailModel.

package demo;
import java.util.*;

public class WeightedNineTailModel extends NineTailModel {
    /** Construct a model */
    public WeightedNineTailModel() {
        // Create edges
        List edges = getEdges();

        // Create a graph
        WeightedGraph graph = new WeightedGraph(edges, NUMBER_OF_NODES);

        // Obtain a shortest path tree rooted at the target node
        tree = graph.getShortestPath(511);
    }

    /** Create all edges for the graph */
    private List getEdges() {
        // Store edges
        List edges = new ArrayList();

        for(int u = 0; u .ShortestPathTree)tree).getCost(u);
    }
}

WeightedNineTailModel estende NineTailModel para construir um WeightedGraph para modelar o problema das nove caudas ponderadas (linhas 10–11). Para cada nó u, o método getEdges() encontra um nó invertido v e atribui o número de inversões como o peso para a aresta (v, você) (linha 30). O método getNumberOfFlips(int u, int v) retorna o número de inversões do nó u para o nó v (linhas 38–47). O número de lançamentos é o número de células diferentes entre o
dois nós (linha 44).

O WeightedNineTailModel obtém um ShortestPathTree enraizado no nó de destino 511 (linha 14). Observe que tree é um campo de dados protegido definido em NineTailModel e ShortestPathTree é uma subclasse de Tree. Os métodos definidos em NineTailModel usam a propriedade tree.

O método getNumberOfFlips(int u) (linhas 49–52) retorna o número de inversões do nó u para o nó de destino, que é o custo do caminho do nó u para o nó de destino. Este custo pode ser obtido invocando o método getCost(u) definido na classe ShortestPathTree (linha 51).

O código abaixo fornece um programa que solicita ao usuário que insira um nó inicial e exibe o número mínimo de giros para alcançar o nó de destino.

package demo;

import java.util.Scanner;

public class WeightedNineTail {

    public static void main(String[] args) {
        // Prompt the user to enter nine coins' Hs and Ts
        System.out.print("Enter the initial nine coins Hs and Ts: ");
        Scanner input = new Scanner(System.in);
        String s = input.nextLine();
        char[] initialNode = s.toCharArray();

        WeightedNineTailModel model = new WeightedNineTailModel();
        java.util.List path = model.getShortestPath(NineTailModel.getIndex(initialNode));

        System.out.println("The steps to flip the coins are ");
        for (int i = 0; i 



Insira nove moedas iniciais Hs e Ts: HHHTTTHHH

As etapas para lançar as moedas são

HHH

TTT

HHH

HHH

TH

TTT

TTT

TTT

TTT

O número de lançamentos é 8

O programa solicita que o usuário insira um nó inicial com nove letras com uma combinação de Hs e Ts como uma string na linha 8, obtém uma matriz de caracteres de a string (linha 9), cria um modelo (linha 11), obtém o caminho mais curto do nó inicial ao nó de destino (linhas 12–13), exibe os nós no caminho (linhas 16–17) e invoca getNumberOfFlips para obter o número de lançamentos necessários para alcançar o nó de destino (linha 20).