JavaScript é frequentemente ridicularizado quando os desenvolvedores encontram pela primeira vez este resultado aparentemente desconcertante:

0.1   0.2 == 0.30000000000000004

Memes sobre o tratamento de números pelo JavaScript são generalizados, muitas vezes levando muitos a acreditar que esse comportamento é exclusivo da linguagem.

No entanto, essa peculiaridade não se limita apenas ao JavaScript. É uma consequência de como a maioria das linguagens de programação lida com aritmética de ponto flutuante.

Por exemplo, aqui estão trechos de código de Java e Go que produzem resultados semelhantes:

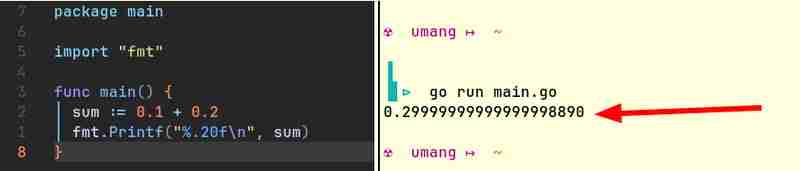
Os computadores podem armazenar nativamente apenas números inteiros. Eles não entendem frações. (Como eles farão? A única maneira de os computadores fazerem aritmética é acendendo ou apagando algumas luzes. A luz pode estar acesa ou apagada. Não pode estar "pela metade" acesa!) Eles precisam de alguma forma de representar números de ponto flutuante . Como esta representação não é perfeitamente precisa, na maioria das vezes, 0,1 0,2 não é igual a 0,3.

Todas as frações cujos denominadores são feitos de fatores primos da base do sistema numérico podem ser expressas de forma limpa, enquanto quaisquer outras frações teriam decimais repetidos. Por exemplo, no sistema numérico com base 10, frações como 1/2, 1/4, 1/5, 1/10 são representadas de forma clara porque os denominadores em cada caso são compostos de 2 ou 5 - os fatores primos de 10 . No entanto, frações como 1/3, 1/6, 1/7 têm decimais recorrentes.

Da mesma forma, no sistema binário frações como 1/2, 1/4, 1/8 são expressas de forma clara, enquanto todas as outras frações têm decimais recorrentes. Quando você realiza aritmética nesses decimais recorrentes, você acaba com sobras que são transportadas quando você converte a representação binária de números do computador em uma representação de base 10 legível por humanos. Isto é o que leva a resultados aproximadamente corretos.

Agora que estabelecemos que esse problema não é exclusivo do JavaScript, vamos explorar como os números de ponto flutuante são representados e processados ​​nos bastidores para entender por que esse comportamento ocorre.

Para entender como os números de ponto flutuante são representados e processados ​​nos bastidores, primeiro teríamos que entender o padrão de ponto flutuante IEEE 754.

O padrão IEEE 754 é uma especificação amplamente usada para representar e realizar aritmética em números de ponto flutuante em sistemas de computador. Foi criado para garantir consistência ao usar aritmética de ponto flutuante em diversas plataformas de computação. A maioria das linguagens de programação e implementações de hardware (CPUs, GPUs, etc.) aderem a este padrão.

É assim que um número é denotado no formato IEEE 754:

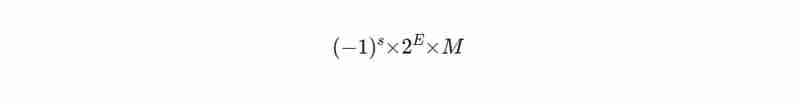
Aqui s é o bit de sinal (0 para positivo, 1 para negativo), M é a mantissa (contém os dígitos do número) e E é o expoente que determina a escala do número.

Você não seria capaz de encontrar nenhum valor inteiro para M e E que pudesse representar exatamente números como 0,1, 0,2 ou 0,3 neste formato. Só podemos escolher valores para M e E que forneçam o resultado mais próximo.

Aqui está uma ferramenta que você pode usar para determinar as notações IEEE 754 de números decimais: https://www.h-schmidt.net/FloatConverter/IEEE754.html

Notação IEEE 754 de 0,25:

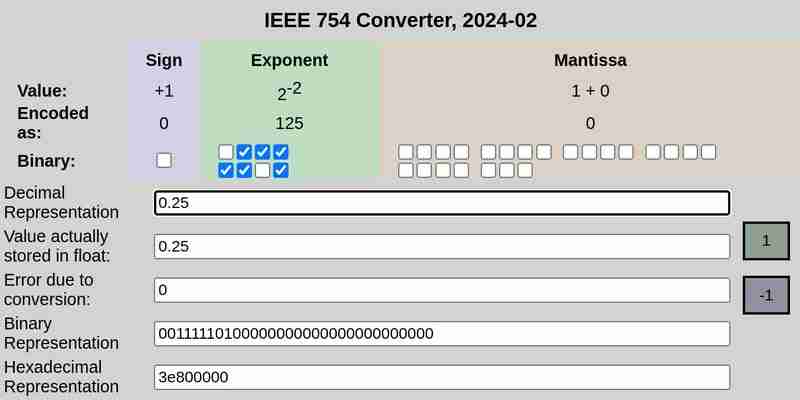
Notação IEEE 754 de 0,1 e 0,2 respectivamente:

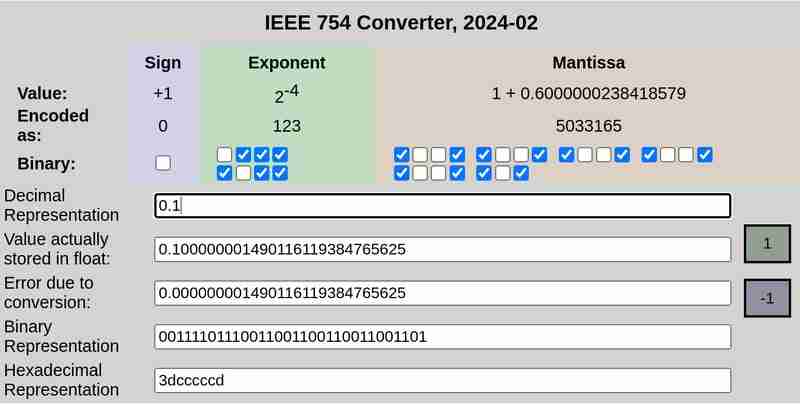
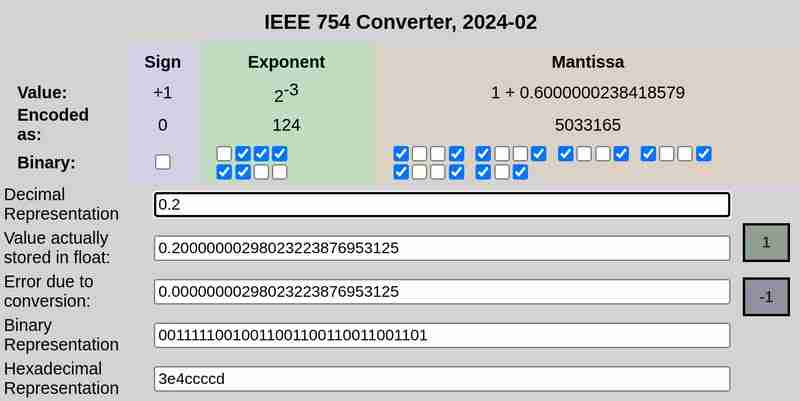
Observe que o erro devido à conversão no caso de 0,25 foi 0, enquanto 0,1 e 0,2 tiveram erros diferentes de zero.

IEEE 754 define os seguintes formatos para representar números de ponto flutuante:

• Precisão simples (32 bits): 1 bit para sinal, 8 bits para expoente, 23 bits para mantissa

• Precisão dupla (64 bits): 1 bit para sinal, 11 bits para expoente, 52 bits para mantissa

Para simplificar, vamos considerar o formato de precisão simples que usa 32 bits.

A representação de 32 bits de 0,1 é:

0 01111011 10011001100110011001101

Aqui o primeiro bit representa o sinal (0 que significa positivo neste caso), os próximos 8 bits (01111011) representam o expoente e os 23 bits finais (10011001100110011001101) representam a mantissa.

Esta não é uma representação exata. Representa ≈ 0,100000001490116119384765625

Da mesma forma, a representação de 32 bits de 0,2 é:

0 01111100 10011001100110011001101

Esta também não é uma representação exata. Representa ≈ 0,20000000298023223876953125

Quando adicionado, resulta em:

0 01111101 11001101010011001100110 

que é ≈ 0,30000001192092896 em representação decimal.

Concluindo, o resultado aparentemente desconcertante de 0,1 0,2 não produzindo 0,3 não é uma anomalia específica do JavaScript, mas uma consequência das limitações da aritmética de ponto flutuante nas linguagens de programação. As raízes desse comportamento estão na representação binária de números, o que leva inerentemente a erros de precisão ao lidar com certas frações.