Muitos problemas do mundo real podem ser resolvidos usando algoritmos gráficos. Os gráficos são úteis na modelagem e resolução de problemas do mundo real. Por exemplo, o problema para encontrar o menor número de voos entre duas cidades pode ser modelado usando um gráfico, onde os vértices representam cidades e as arestas representam os voos entre duas cidades adjacentes, conforme mostrado na figura abaixo. O problema de encontrar o número mínimo de voos de conexão
entre duas cidades se reduz a encontrar o caminho mais curto entre dois vértices em um gráfico.

O estudo de problemas de grafos é conhecido como teoria dos grafos. A teoria dos grafos foi fundada por Leonhard Euler em 1736, quando ele introduziu a terminologia dos grafos para resolver o famoso problema das Sete Pontes de Königsberg. A cidade de Königsberg, na Prússia (atual Kaliningrado, na Rússia), foi dividida pelo rio Pregel. Havia duas ilhas no rio. A cidade e as ilhas eram ligadas por sete pontes, conforme mostra a figura abaixo (a). A questão é: é possível dar um passeio, atravessar cada ponte exatamente uma vez e voltar ao ponto de partida? Euler provou que isso não é possível.

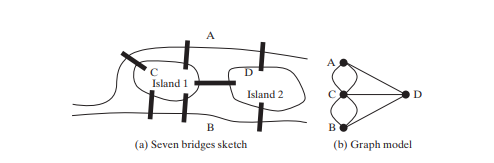
Para estabelecer uma prova, Euler primeiro abstraiu o mapa da cidade de Königsberg eliminando todas as ruas, produzindo o esboço mostrado na Figura acima (a). Em seguida, ele substituiu cada massa de terra por um ponto, chamado vértice ou nó, e cada ponte por uma linha, chamada aresta, como mostrado em Figura acima (b). Essa estrutura com vértices e arestas é chamada de grafo.

Olhando para o gráfico, perguntamos se existe um caminho começando em qualquer vértice, atravessando todas as arestas exatamente uma vez e retornando ao vértice inicial. Euler provou que para que tal caminho exista, cada vértice deve ter um número par de arestas. Portanto, o problema das Sete Pontes de Königsberg não tem solução.

Problemas gráficos geralmente são resolvidos usando algoritmos. Algoritmos de grafos têm muitas aplicações em diversas áreas, como ciência da computação, matemática, biologia, engenharia, economia, genética e ciências sociais.

Terminologias básicas de gráficos

Um gráfico consiste em vértices e arestas que conectam os vértices. Este capítulo não pressupõe que você tenha qualquer conhecimento prévio de teoria dos grafos ou matemática discreta. Usamos termos claros e simples para definir gráficos.

O que é um gráfico? Um gráfico é uma estrutura matemática que representa relacionamentos entre entidades no mundo real. Por exemplo, o gráfico da Figura acima representa os voos entre cidades, e o gráfico da Figura abaixo (b) representa as pontes entre massas de terra.

Um gráfico consiste em um conjunto não vazio de vértices (também conhecidos como nós ou pontos) e um conjunto de arestas que conectam os vértices. Por conveniência, definimos um gráfico como G = (V, E), onde V representa um conjunto de vértices e E representa um conjunto de arestas. Por exemplo, V e E para o gráfico da Figura abaixo são os seguintes:

V = {"Seattle", "São Francisco", "Los Angeles",
"Denver", "Kansas City", "Chicago", "Boston", "Nova York",
"Atlanta", "Miami", "Dallas", "Houston"};

E = {{"Seattle", "São Francisco"},{"Seattle", "Chicago"},
{"Seattle", "Denver"}, {"São Francisco", "Denver"},
...
};

Um gráfico pode ser direcionado ou não direcionado. Em um grafo direcionado, cada aresta tem uma direção, o que indica que você pode se mover de um vértice para outro através da aresta. Você pode modelar relacionamentos pai/filho usando um gráfico direcionado, onde uma aresta do vértice A a B indica que A é pai de B. A figura abaixo (a) mostra um gráfico direcionado.

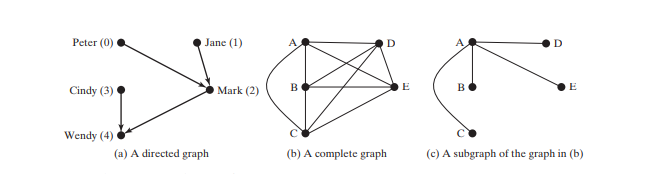
Em um gráfico não direcionado, você pode se mover em ambas as direções entre vértices. O gráfico na figura abaixo não é direcionado.

As arestas podem ser ponderadas ou não. Por exemplo, você pode atribuir um peso para cada aresta no gráfico da Figura acima para indicar o tempo de voo entre as duas cidades.

Dois vértices em um gráfico são considerados adjacentes se estiverem conectados pela mesma aresta. Da mesma forma, duas arestas são consideradas adjacentes se estiverem conectadas ao mesmo vértice. Uma aresta em um gráfico que une dois vértices é considerada incidente em ambos os vértices. O grau de um vértice é o número de arestas incidentes a ele.

Dois vértices são chamados de vizinhos se forem adjacentes. Da mesma forma, duas arestas são chamadas de vizinhas se forem adjacentes.

Um loop é uma aresta que liga um vértice a si mesmo. Se dois vértices são conectados por duas ou mais arestas, essas arestas são chamadas de arestas paralelas. Um gráfico simples é aquele que não possui loops ou arestas paralelas. Em um grafo completo, cada dois pares de vértices são conectados, conforme mostrado na Figura abaixo (b).

Um gráfico é conectado se existir um caminho entre quaisquer dois vértices no gráfico. Um subgrafo de um grafo G é um grafo cujo conjunto de vértices é um subconjunto daquele de G e cujo conjunto de arestas é um subconjunto daquele de G. Por exemplo, o gráfico na Figura acima (c) é um subgrafo do gráfico na Figura acima (b).

Suponha que o gráfico seja conectado e não direcionado. Um ciclo é um caminho fechado que começa em um vértice e termina no mesmo vértice. Um gráfico conectado é uma árvore se não tiver ciclos. Uma árvore geradora de um grafo G é um subgrafo conectado de G e o subgrafo é uma árvore que contém todos os vértices de G.