Introdução

Neste artigo, demonstraremos um fluxo de trabalho completo de projeto de aprendizado de máquina usando Scikit-Learn. Construiremos um modelo para prever os preços das moradias na Califórnia com base em vários recursos, como renda média, idade da casa e número médio de quartos. Este projeto irá guiá-lo em cada etapa do processo, incluindo carregamento de dados, exploração, treinamento de modelo, avaliação e visualização de resultados. Quer você seja um iniciante em busca de entender o básico ou um profissional experiente em busca de uma atualização, este artigo fornecerá informações valiosas sobre a aplicação prática de técnicas de aprendizado de máquina.

Projeto de previsão de preços de habitação na Califórnia

1. Introdução

O mercado imobiliário da Califórnia é conhecido por suas características únicas e dinâmica de preços. Neste projeto, pretendemos desenvolver um modelo de aprendizado de máquina para prever preços de casas com base em vários recursos. Usaremos o conjunto de dados habitacionais da Califórnia, que inclui vários atributos, como renda média, idade da casa, quartos médios e muito mais.

2. Importando Bibliotecas

Nesta seção, importaremos as bibliotecas necessárias para manipulação de dados, visualização e construção de nosso modelo de aprendizado de máquina.

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.datasets import fetch_california_housing

3. Carregando o conjunto de dados

Carregaremos o conjunto de dados California Housing e criaremos um DataFrame para organizar os dados. A variável alvo, que é o preço da casa, será adicionada como uma nova coluna.

# Load the California Housing dataset
california = fetch_california_housing()
df = pd.DataFrame(california.data, columns=california.feature_names)
df['PRICE'] = california.target

4. Seleção aleatória de amostras

Para manter a análise gerenciável, selecionaremos aleatoriamente 700 amostras do conjunto de dados para nosso estudo.

# Randomly Selecting 700 Samples
df_sample = df.sample(n=700, random_state=42)

5. Analisando nossos dados

Esta seção fornecerá uma visão geral do conjunto de dados, exibindo as primeiras cinco linhas para entender os recursos e a estrutura de nossos dados.

# Overview of the data
print("First five rows of the dataset:")
print(df_sample.head())

Saída

First five rows of the dataset:
       MedInc  HouseAge  AveRooms  AveBedrms  Population  AveOccup  Latitude  \
20046  1.6812      25.0  4.192201   1.022284      1392.0  3.877437     36.06   
3024   2.5313      30.0  5.039384   1.193493      1565.0  2.679795     35.14   
15663  3.4801      52.0  3.977155   1.185877      1310.0  1.360332     37.80   
20484  5.7376      17.0  6.163636   1.020202      1705.0  3.444444     34.28   
9814   3.7250      34.0  5.492991   1.028037      1063.0  2.483645     36.62   

       Longitude    PRICE  
20046    -119.01  0.47700  
3024     -119.46  0.45800  
15663    -122.44  5.00001  
20484    -118.72  2.18600  
9814     -121.93  2.78000  

Exibir informações do DataFrame

print(df_sample.info())

Saída

Index: 700 entries, 20046 to 5350
Data columns (total 9 columns):
 #   Column      Non-Null Count  Dtype  
---  ------      --------------  -----  
 0   MedInc      700 non-null    float64
 1   HouseAge    700 non-null    float64
 2   AveRooms    700 non-null    float64
 3   AveBedrms   700 non-null    float64
 4   Population  700 non-null    float64
 5   AveOccup    700 non-null    float64
 6   Latitude    700 non-null    float64
 7   Longitude   700 non-null    float64
 8   PRICE       700 non-null    float64
dtypes: float64(9)
memory usage: 54.7 KB

Exibir estatísticas resumidas

print(df_sample.describe())

Saída

           MedInc    HouseAge    AveRooms   AveBedrms   Population  \
count  700.000000  700.000000  700.000000  700.000000   700.000000   
mean     3.937653   28.855714    5.404192    1.079266  1387.422857   
std      2.085831   12.353313    1.848898    0.236318  1027.873659   
min      0.852700    2.000000    2.096692    0.500000     8.000000   
25%      2.576350   18.000000    4.397751    1.005934   781.000000   
50%      3.480000   30.000000    5.145295    1.047086  1159.500000   
75%      4.794625   37.000000    6.098061    1.098656  1666.500000   
max     15.000100   52.000000   36.075472    5.273585  8652.000000   

         AveOccup    Latitude   Longitude       PRICE  
count  700.000000  700.000000  700.000000  700.000000  
mean     2.939913   35.498243 -119.439729    2.082073  
std      0.745525    2.123689    1.956998    1.157855  
min      1.312994   32.590000 -124.150000    0.458000  
25%      2.457560   33.930000 -121.497500    1.218500  
50%      2.834524   34.190000 -118.420000    1.799000  
75%      3.326869   37.592500 -118.007500    2.665500  
max      7.200000   41.790000 -114.590000    5.000010  

6. Dividindo o conjunto de dados em conjuntos de treinamento e teste

Separaremos o conjunto de dados em recursos (X) e a variável de destino (y) e, em seguida, dividiremos em conjuntos de treinamento e teste para treinamento e avaliação do modelo.

# Splitting the dataset into Train and Test sets
X = df_sample.drop('PRICE', axis=1)  # Features
y = df_sample['PRICE']  # Target variable

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

7. Treinamento de modelo

Nesta seção, criaremos e treinaremos um modelo de regressão linear usando os dados de treinamento para aprender a relação entre recursos e preços de casas.

# Creating and training the Linear Regression model
lr = LinearRegression()
lr.fit(X_train, y_train)

8. Avaliando o Modelo

Faremos previsões no conjunto de teste e calcularemos o erro quadrático médio (MSE) e os valores de R ao quadrado para avaliar o desempenho do modelo.

# Making predictions on the test set
y_pred = lr.predict(X_test)

# Calculating Mean Squared Error
mse = mean_squared_error(y_test, y_pred)
print(f"\nLinear Regression Mean Squared Error: {mse}")

Saída

Linear Regression Mean Squared Error: 0.3699851092128846

9. Exibindo valores reais versus valores previstos

Aqui, criaremos um DataFrame para comparar os preços reais das casas com os preços previstos gerados pelo nosso modelo.

# Displaying Actual vs Predicted Values
results = pd.DataFrame({'Actual Prices': y_test.values, 'Predicted Prices': y_pred})
print("\nActual vs Predicted:")
print(results)

Saída

Actual vs Predicted:
     Actual Prices  Predicted Prices
0          0.87500          0.887202
1          1.19400          2.445412
2          5.00001          6.249122
3          2.78700          2.743305
4          1.99300          2.794774
..             ...               ...
135        1.62100          2.246041
136        3.52500          2.626354
137        1.91700          1.899090
138        2.27900          2.731436
139        1.73400          2.017134

[140 rows x

 2 columns]

10. Visualizando os Resultados

Na seção final, visualizaremos a relação entre os preços reais e previstos das casas usando um gráfico de dispersão para avaliar visualmente o desempenho do modelo.

# Visualizing the Results
plt.figure(figsize=(8, 6))
plt.scatter(y_test, y_pred, color='blue')
plt.xlabel('Actual Prices')
plt.ylabel('Predicted Prices')
plt.title('Actual vs Predicted House Prices')

# Draw the ideal line
plt.plot([0, 6], [0, 6], color='red', linestyle='--')

# Set limits to minimize empty space
plt.xlim(y_test.min() - 1, y_test.max()   1)
plt.ylim(y_test.min() - 1, y_test.max()   1)

plt.grid()
plt.show()

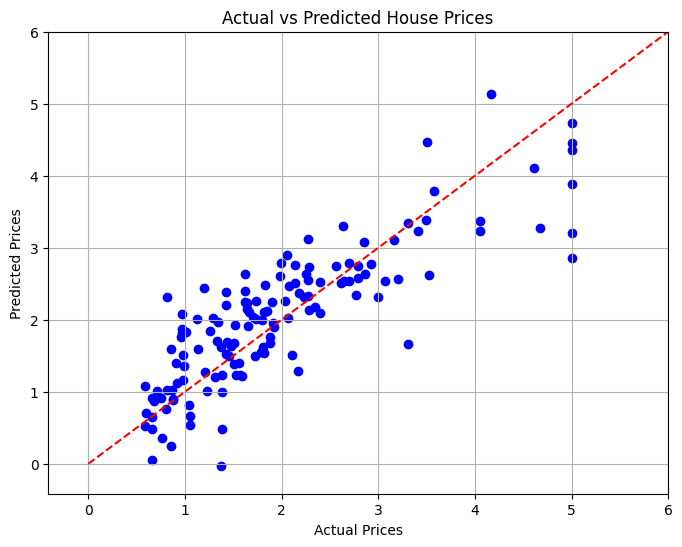
Conclusão

Neste projeto, desenvolvemos um modelo de regressão linear para prever os preços das moradias na Califórnia com base em vários recursos. O erro quadrático médio foi calculado para avaliar o desempenho do modelo, o que forneceu uma medida quantitativa da precisão da predição. Por meio da visualização, pudemos ver o desempenho do nosso modelo em relação aos valores reais.

Este projeto demonstra o poder do aprendizado de máquina na análise imobiliária e pode servir como base para técnicas de modelagem preditiva mais avançadas.