자, 이야기는 이렇습니다. 저는 최근 Zhuang 교수의 학교 과제에서 Incremental Association Markov Blanket(IAMB)라는 매우 멋진 알고리즘을 사용하는 작업을 수행했습니다. 저는 데이터 과학이나 통계에 대한 배경 지식이 없기 때문에 이것은 저에게 새로운 영역이지만 새로운 것을 배우는 것을 좋아합니다. 목표는? IAMB를 사용하여 데이터세트에서 기능을 선택하고 이것이 머신러닝 모델의 성능에 어떤 영향을 미치는지 확인하세요.

IAMB 알고리즘의 기본 사항을 살펴보고 이를 Jason Brownlee의 데이터 세트의 Pima Indians Diabetes 데이터 세트에 적용하겠습니다. 이 데이터 세트는 여성의 건강 데이터를 추적하고 당뇨병 여부를 포함합니다. 우리는 IAMB를 사용하여 당뇨병 예측에 가장 중요한 특징(BMI 또는 혈당 수치 등)을 알아낼 것입니다.

IAMB 알고리즘은 무엇이며 왜 사용합니까?

IAMB 알고리즘은 수수께끼 속의 용의자 목록을 정리하는 데 도움을 주는 친구와 같습니다. 목표를 예측하는 데 정말로 중요한 변수만 골라내도록 설계된 특징 선택 방법입니다. 이 경우 대상은 당뇨병 여부입니다.

• 전진 단계: 대상과 밀접한 관련이 있는 변수를 추가합니다.
• 후진 단계: 실제로 도움이 되지 않는 변수를 잘라내고 가장 중요한 변수만 남도록 합니다.

간단히 말하면 IAMB는 가장 관련성이 높은 기능만 선택하여 데이터 세트가 복잡해지는 것을 방지하는 데 도움이 됩니다. 이는 모델 성능을 단순하게 유지하고 훈련 시간을 단축하려는 경우 특히 유용합니다.

출처: 대규모 마르코프 담요 발견을 위한 알고리즘

이 알파 기능은 무엇이며 왜 중요한가요?

여기서 알파가 필요합니다. 통계에서 알파(α)는 "통계적으로 유의미한" 항목을 결정하기 위해 설정한 임계값입니다. 교수가 제공한 지침의 일부로 알파 0.05를 사용했습니다. 즉, 대상 변수와 무작위로 연관될 확률이 5% 미만인 특성만 유지하고 싶다는 뜻입니다. 따라서 특성의 p-값이 0.05보다 작다면 이는 목표와 강력하고 통계적으로 유의미한 연관성이 있음을 의미합니다.

이 알파 임계값을 사용하여 가장 의미 있는 변수에만 초점을 맞추고 "유의성" 테스트를 통과하지 못한 변수는 무시합니다. 가장 관련성이 높은 기능은 유지하고 노이즈는 걸러내는 필터와 같습니다.

실습: Pima Indians 당뇨병 데이터 세트에서 IAMB 사용

설정은 다음과 같습니다. Pima Indians 당뇨병 데이터 세트에는 건강 기능(혈압, 연령, 인슐린 수치 등)과 목표 결과(당뇨병 발병 여부)가 있습니다.

먼저 데이터를 로드하고 확인합니다.

import pandas as pd
# Load and preview the dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv'
column_names = ['Pregnancies', 'Glucose', 'BloodPressure', 'SkinThickness', 'Insulin', 'BMI', 'DiabetesPedigreeFunction', 'Age', 'Outcome']
data = pd.read_csv(url, names=column_names)
print(data.head())

Alpha = 0.05로 IAMB 구현

다음은 IAMB 알고리즘의 업데이트된 버전입니다. 우리는 p-값을 사용하여 유지할 특성을 결정하므로 p-값이 알파(0.05)보다 작은 특성만 선택됩니다.

import pingouin as pg
def iamb(target, data, alpha=0.05):
    markov_blanket = set()
    # Forward Phase: Add features with a p-value  alpha
    for feature in list(markov_blanket):
        reduced_mb = markov_blanket - {feature}
        result = pg.partial_corr(data=data, x=feature, y=target, covar=reduced_mb)
        p_value = result.at[0, 'p-val']
        if p_value > alpha:
            markov_blanket.remove(feature)
    return list(markov_blanket)

# Apply the updated IAMB function on the Pima dataset
selected_features = iamb('Outcome', data, alpha=0.05)
print("Selected Features:", selected_features)

이 프로그램을 실행했을 때 IAMB가 당뇨병 결과와 가장 밀접하게 관련되어 있다고 생각하는 기능의 세련된 목록이 제공되었습니다. 이 목록은 모델을 구축하는 데 필요한 변수의 범위를 좁히는 데 도움이 됩니다.

Selected Features: ['BMI', 'DiabetesPedigreeFunction', 'Pregnancies', 'Glucose']

IAMB가 선택한 기능이 모델 성능에 미치는 영향 테스트

선택한 기능이 있으면 실제 테스트에서는 모든 기능과 IAMB에서 선택한 기능의 모델 성능을 비교합니다. 이를 위해 간단한 Gaussian Naive Bayes 모델을 사용했습니다. 왜냐하면 이 모델은 간단하고 (전체 베이지안 분위기와 관련이 있는) 확률과 잘 어울리기 때문입니다.

모델을 학습하고 테스트하는 코드는 다음과 같습니다.

from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score, f1_score, roc_auc_score

# Split data
X = data.drop('Outcome', axis=1)
y = data['Outcome']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Model with All Features
model_all = GaussianNB()
model_all.fit(X_train, y_train)
y_pred_all = model_all.predict(X_test)

# Model with IAMB-Selected Features
X_train_selected = X_train[selected_features]
X_test_selected = X_test[selected_features]

model_iamb = GaussianNB()
model_iamb.fit(X_train_selected, y_train)
y_pred_iamb = model_iamb.predict(X_test_selected)

# Evaluate models
results = {
    'Model': ['All Features', 'IAMB-Selected Features'],
    'Accuracy': [accuracy_score(y_test, y_pred_all), accuracy_score(y_test, y_pred_iamb)],
    'F1 Score': [f1_score(y_test, y_pred_all, average='weighted'), f1_score(y_test, y_pred_iamb, average='weighted')],
    'AUC-ROC': [roc_auc_score(y_test, y_pred_all), roc_auc_score(y_test, y_pred_iamb)]
}

results_df = pd.DataFrame(results)
display(results_df)

결과

비교 내용은 다음과 같습니다.

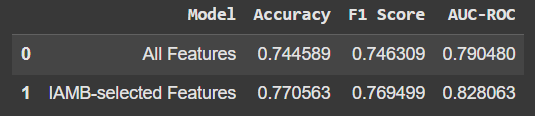
IAMB가 선택한 기능만 사용하면 정확도와 기타 측정항목이 약간 향상되었습니다. 큰 발전은 아니지만 더 적은 수의 기능으로 더 나은 성능을 얻을 수 있다는 사실은 유망합니다. 게다가 이는 우리 모델이 '노이즈'나 관련 없는 데이터에 의존하지 않는다는 것을 의미합니다.

주요 시사점

• IAMB는 기능 선택에 적합합니다: 목표를 예측하는 데 정말로 중요한 것에만 집중하여 데이터 세트를 정리하는 데 도움이 됩니다.
• 적을수록 더 많은 경우가 많습니다: 여기서 본 것처럼 모델 정확도가 약간 향상되는 것처럼 특성이 적을수록 더 나은 결과를 얻을 수도 있습니다.
• 학습과 실험은 재미있는 부분입니다: 데이터 과학에 대한 깊은 배경 지식이 없더라도 이와 같은 프로젝트에 참여하면 데이터와 기계 학습을 이해하는 새로운 방법이 열립니다.

이것이 IAMB에 대한 친근한 소개가 되기를 바랍니다! 궁금하다면 한번 시도해 보세요. 기계 학습 도구 상자에 있는 편리한 도구이며 자신의 프로젝트에서 몇 가지 멋진 개선 사항을 확인할 수도 있습니다.

출처: 대규모 마르코프 담요 발견을 위한 알고리즘