グラフの深さ優先検索は、グラフ内の頂点から開始し、バックトラックする前に可能な限りグラフ内のすべての頂点を訪問します。
グラフの深さ優先検索は、ツリー トラバーサル、ツリー トラバーサルで説明したツリーの深さ優先検索に似ています。ツリーの場合、ルートから検索が開始されます。グラフでは、任意の頂点から検索を開始できます。

ツリーの深さ優先検索では、まずルートにアクセスし、次にルートのサブツリーに再帰的にアクセスします。同様に、グラフの深さ優先検索は最初に頂点を訪問し、次にその頂点に隣接するすべての頂点を再帰的に訪問します。違いは、グラフにサイクルが含まれる可能性があり、無限再帰につながる可能性があることです。この問題を回避するには、すでに訪問した頂点を追跡する必要があります。

検索は、グラフ内で可能な限り「深く」検索するため、深さ優先と呼ばれます。検索はある頂点 v から始まります。v を訪問した後、v の未訪問の近傍を訪問します。v に未訪問の近傍がない場合、検索は v に到達した頂点に戻ります。グラフが接続されており、検索が開始されると仮定します。任意の頂点からすべての頂点に到達できます。

深さ優先検索アルゴリズム

深さ優先検索のアルゴリズムは、以下のコードで説明されています。

入力: G = (V, E) および開始頂点 v
出力: v
をルートとする DFS ツリー 1 ツリー dfs(頂点 v) {
2 訪問 v;
v
の近隣 w ごとに 3 4 if (w が訪問されていない) {
5 v をツリー内の w の親として設定します;
6 dfs(w);
7 }
8 }

isVisited という名前の配列を使用して、頂点が訪問されたかどうかを示すことができます。最初は、各頂点 i の isVisited[i] は false です。頂点、たとえば v が訪問されると、isVisited[v] は true に設定されます。

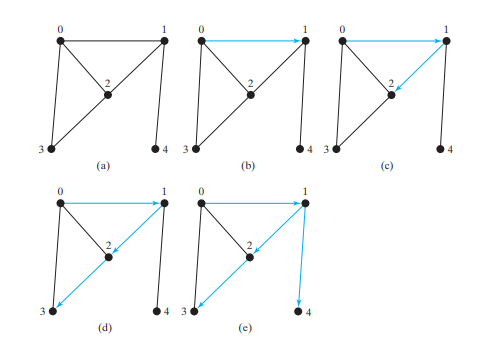
下の図 (a) のグラフを考えてみましょう。頂点 0 から深さ優先検索を開始するとします。最初に 0 を訪問し、次にその近隣のいずれか (たとえば 1) を訪問します。次の図 (b) に示すように、今度は 1 が訪問されます。頂点 1 には 3 つの近傍 (0、2、および 4) があります。0 はすでに訪問されているため、2 または 4 のいずれかを訪問します。2 を選択しましょう。次の図 (c) に示すように、現在 2 が訪問されています。頂点 2 には、0、1、および 3 という 3 つの近傍があります。0 と 1 はすでに訪問されているため、3 を選択します。下の図 (d) に示すように、3 が訪問されます。この時点で、頂点は次の順序で訪問されています:

0、1、2、3

3 の近傍をすべて訪問したので、2 に戻ります。2 の頂点をすべて訪問したので、1 に戻ります。4 は 1 に隣接していますが、4 は訪問されていません。したがって、次の図 (e) に​​示すように、4 にアクセスします。 4 の近隣すべてを訪問したので、1 に戻ります。
1 のすべての近傍を訪問したため、0 に戻ります。0 のすべての近傍を訪問したため、検索は終了します。

各エッジと各頂点は 1 回だけ訪問されるため、dfs メソッドの時間計算量は O(|E| |V|) になります。ここで、|E | はエッジの数を示し、|V| は頂点の数を示します。

深さ優先検索の実装

上記のコードの DFS のアルゴリズムは再帰を使用します。それを実装するには再帰を使用するのが自然です。あるいは、スタックを使用することもできます。

dfs(int v) メソッドは、AbstractGraph.java の 164 ～ 193 行目に実装されています。これは、頂点 v をルートとする Tree クラスのインスタンスを返します。このメソッドは、検索された頂点をリスト searchOrder (165 行目) に格納し、各頂点の親を配列 parent (166 行目) に格納し、isVisited 頂点が訪問されたかどうかを示す配列 (行 171)。これは、ヘルパー メソッド dfs(v,parent,searchOrder,isVisited) を呼び出して、深さ優先検索を実行します (174 行目)。

再帰ヘルパー メソッドでは、頂点

u から検索が開始されます。 u は 184 行目で searchOrder に追加され、訪問済みとしてマークされます (185 行目)。 u の未訪問の各近傍に対して、このメソッドが再帰的に呼び出され、深さ優先検索が実行されます。頂点 e.v にアクセスすると、e.v の親が parent[e.v] に格納されます (189 行目)。このメソッドは、接続されたグラフまたは接続されたコンポーネントのすべての頂点にアクセスすると戻ります。

以下のコードは、シカゴから始まる上図のグラフの DFS を表示するテスト プログラムを提供します。シカゴから始まる DFS の図を下の図に示します。

パブリック クラス TestDFS { public static void main(String[] args) { String[] 頂点 = {"シアトル"、"サンフランシスコ"、"ロサンゼルス"、"デンバー"、"カンザスシティ"、"シカゴ"、"ボストン"、"ニューヨーク"、"アトランタ"、"マイアミ"、 "ダラス"、"ヒューストン"}; int[][] エッジ = { {0, 1}、{0, 3}、{0, 5}、 {1, 0}、{1, 2}、{1, 3}、 {2, 1}、{2, 3}、{2, 4}、{2, 10}、 {3, 0}、{3, 1}、{3, 2}、{3, 4}、{3, 5}、 {4, 2}、{4, 3}、{4, 5}、{4, 7}、{4, 8}、{4, 10}、 {5, 0}、{5, 3}、{5, 4}、{5, 6}、{5, 7}、 {6, 5}、{6, 7}、 {7, 4}、{7, 5}、{7, 6}、{7, 8}、 {8, 4}、{8, 7}、{8, 9}、{8, 10}、{8, 11}、 {9、8}、{9、11}、 {10, 2}、{10, 4}、{10, 8}、{10, 11}、 {11, 8}、{11, 9}、{11, 10} }; Graph グラフ = new UnweightedGraph(頂点, エッジ); AbstractGraph.Tree dfs =graph.dfs(graph.getIndex("シカゴ")); java.util.List searchOrders = dfs.getSearchOrder(); System.out.println(dfs.getNumberOfVerticesFound() " 頂点はこの DFS 順序で検索されます:"); for(int i = 0; i public class TestDFS { public static void main(String[] args) { String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"}; int[][] edges = { {0, 1}, {0, 3}, {0, 5}, {1, 0}, {1, 2}, {1, 3}, {2, 1}, {2, 3}, {2, 4}, {2, 10}, {3, 0}, {3, 1}, {3, 2}, {3, 4}, {3, 5}, {4, 2}, {4, 3}, {4, 5}, {4, 7}, {4, 8}, {4, 10}, {5, 0}, {5, 3}, {5, 4}, {5, 6}, {5, 7}, {6, 5}, {6, 7}, {7, 4}, {7, 5}, {7, 6}, {7, 8}, {8, 4}, {8, 7}, {8, 9}, {8, 10}, {8, 11}, {9, 8}, {9, 11}, {10, 2}, {10, 4}, {10, 8}, {10, 11}, {11, 8}, {11, 9}, {11, 10} }; Graph graph = new UnweightedGraph(vertices, edges); AbstractGraph.Tree dfs = graph.dfs(graph.getIndex("Chicago")); java.util.List searchOrders = dfs.getSearchOrder(); System.out.println(dfs.getNumberOfVerticesFound() " vertices are searched in this DFS order:"); for(int i = 0; i 12 個の頂点が次の DFS 順序で検索されます:

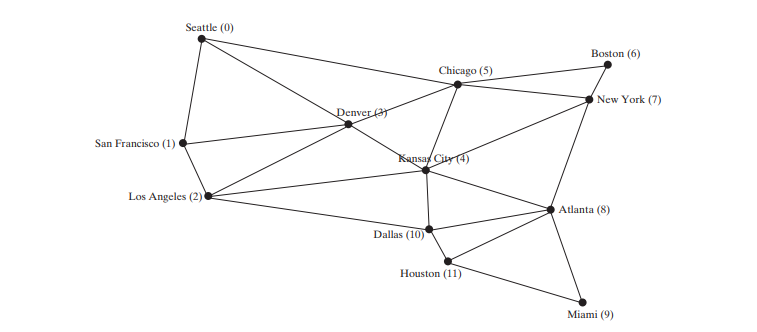
シカゴ シアトル サンフランシスコ ロサンゼルス デンバー
カンザスシティ ニューヨーク ボストン アトランタ マイアミ ヒューストン ダラス
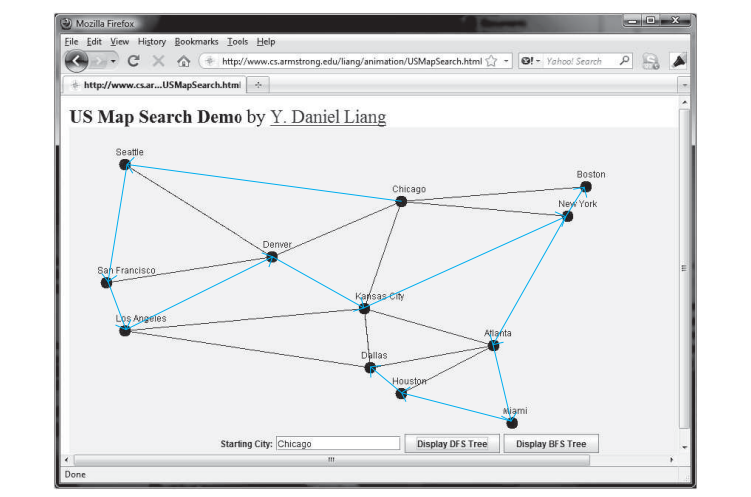
シアトルの親はシカゴです
サンフランシスコの親はシアトルです
ロサンゼルスの親はサンフランシスコ
デンバーの親はロサンゼルスです
カンザスシティの親はデンバーです
ボストンの親はニューヨークです
ニューヨークの親はカンザスシティです
アトランタの親はニューヨーク
マイアミの親はアトランタです
ダラスの親はヒューストン
ヒューストンの親はマイアミです

DFS のアプリケーション

深さ優先検索を使用すると、次のような多くの問題を解決できます:

グラフがつながっているかどうかを検出します。任意の頂点からグラフを検索します。検索された頂点の数がグラフの頂点の数と同じ場合、グラフは接続されます。それ以外の場合、グラフは接続されません。
2 つの頂点間にパスがあるかどうかを検出します。
2 つの頂点間のパスを検索します。
接続されているすべてのコンポーネントを検索します。連結コンポーネントは、頂点のすべてのペアがパスによって接続されている最大連結部分グラフです。
グラフに周期があるかどうかを検出します。
グラフ内のサイクルを見つけます。
ハミルトニアン パス/サイクルを検索します。グラフ内の
• ハミルトニアン パス は、グラフ内の各頂点を 1 回だけ訪問するパスです。 ハミルトニアン サイクルは、グラフ内の各頂点を正確に 1 回訪問し、開始頂点に戻ります。

最初の 6 つの問題は、AbstractGraph.java の dfs メソッドを使用して簡単に解決できます。ハミルトニアン パス/サイクルを見つけるには、考えられるすべての DFS を探索して、最長のパスにつながる DFS を見つける必要があります。ハミルトニアン パス/サイクルには、よく知られているナイツ ツアー問題の解決など、多くの用途があります。