अधिकतम उपसरणी समस्या और उसका इतिहास

1970 के दशक के उत्तरार्ध में, स्वीडिश गणितज्ञ उल्फ ग्रेनांडर एक समस्या पर चर्चा कर रहे थे: आप छवि डेटा की 2डी सरणी का विश्लेषण ब्रूट फोर्स की तुलना में अधिक कुशलता से कैसे कर सकते हैं? तब कंप्यूटर धीमे थे और तस्वीरें रैम के सापेक्ष बड़ी थीं। चीजों को बदतर बनाने के लिए, सबसे खराब स्थिति में क्रूर बल ने O(n^6) समय (सेक्सटिक टाइम जटिलता) लिया।

सबसे पहले, ग्रेनांडियर ने प्रश्न को सरल बनाया: संख्याओं की केवल एक आयामी सरणी को देखते हुए, आप सबसे बड़ी राशि के साथ सन्निहित उपसरणी को सबसे कुशलता से कैसे ढूंढेंगे?

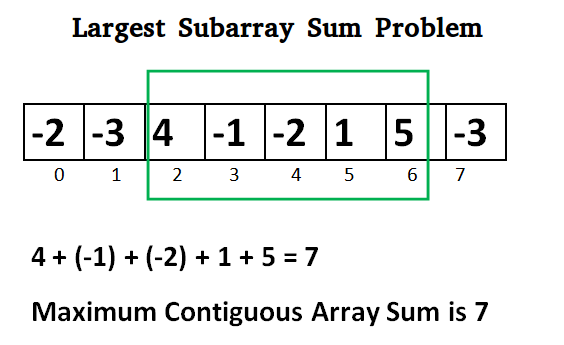
क्रूर बल: घन समय जटिलता के साथ एक अनुभवहीन दृष्टिकोण

बलपूर्वक, एक 1डी सरणी का 2डी सरणी के रूप में विश्लेषण करने में आधा समय लगेगा, इसलिए हर संभावित संयोजन (घन समय जटिलता) की जांच करने के लिए ओ(एन^3)।

def max_subarray_brute_force(arr):
    max_sum = arr[0] # assumes arr has a length

    # iterate over all possible subarrays
    for i in range(len(arr)):
        for j in range(i, len(arr)):
            current_sum = 0
            # sum the elements of the subarray arr[i:j 1]
            for k in range(i, j   1):
                current_sum  = arr[k]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

print(max_subarray_brute_force([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

ग्रेनेंडर का O(n²) अनुकूलन: एक कदम आगे

ग्रेनेंडर ने इसे O(n^2) समाधान में सुधार दिया। मुझे अपने शोध में उसका कोड नहीं मिला, लेकिन मेरा अनुमान है कि उसने बस उस अंतरतम लूप से छुटकारा पा लिया है जो दोनों सूचकांकों के बीच की सभी संख्याओं को जोड़ता है। इसके बजाय, हम उपसरणी पर पुनरावृत्ति करते हुए एक चालू योग रख सकते हैं, इस प्रकार लूप की संख्या तीन से घटाकर दो कर सकते हैं।

def max_subarray_optimized(arr):
    max_sum = arr[0]  # assumes arr has a length

    # iterate over all possible starting points of the subarray
    for i in range(len(arr)):
        current_sum = 0
        # sum the elements of the subarray starting from arr[i]
        for j in range(i, len(arr)):
            current_sum  = arr[j]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

शामोस का फूट डालो और जीतो: O(n log n) के लिए समस्या को विभाजित करना

ग्रेनेंडर ने कंप्यूटर वैज्ञानिक माइकल शामोस को समस्या दिखाई। शामोस ने इसके बारे में एक रात सोचा और फूट डालो और जीतो की एक विधि लेकर आए जो O(n log n) है।

यह काफी चतुर है। विचार यह है कि सरणी को दो हिस्सों में विभाजित किया जाए, फिर प्रत्येक आधे के लिए अधिकतम उपसरणी योग के साथ-साथ मध्यबिंदु को पार करने वाली उपसरणी का पुनरावर्ती पता लगाया जाए।

def max_crossing_sum(arr, left, mid, right):
    # left of mid
    left_sum = float('-inf')
    current_sum = 0
    for i in range(mid, left - 1, -1):
        current_sum  = arr[i]
        left_sum = max(left_sum, current_sum)

    # right of mid
    right_sum = float('inf')
    current_sum = 0
    for i in range(mid   1, right   1):
        current_sum  = arr[i]
        right_sum = max(right_sum, current_sum)

    # sum of elements on the left and right of mid, which is the maximum sum that crosses the midpoint
    return left_sum   right_sum

def max_subarray_divide_and_conquer(arr, left, right):
    # base case: only one element
    if left == right:
        return arr[left]

    # find the midpoint
    mid = (left   right) // 2

    # recursively find the maximum subarray sum for the left and right halves
    left_sum = max_subarray_divide_and_conquer(arr, left, mid)
    right_sum = max_subarray_divide_and_conquer(arr, mid   1, right)
    cross_sum = max_crossing_sum(arr, left, mid, right)

    # return the maximum of the three possible cases
    return max(left_sum, right_sum, cross_sum)

def max_subarray(arr):
    return max_subarray_divide_and_conquer(arr, 0, len(arr) - 1)


print(max_subarray([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

यह समय की जटिलता को घटाकर O(nlogn) कर देता है क्योंकि पहले सरणी को दो हिस्सों (O(logn)) में विभाजित किया जाता है और फिर अधिकतम क्रॉसिंग सबरे को खोजने में O(n) लगता है

कडेन का एल्गोरिदम: द एलिगेंट ओ(एन) सॉल्यूशन

स्टैस्टिशियन जे कडाने ने कोड को देखा और तुरंत पहचान लिया कि शामोस का समाधान समाधान के हिस्से के रूप में सन्निहित संयम का उपयोग करने में विफल रहा।

उसे यह एहसास हुआ

-यदि किसी सरणी में केवल नकारात्मक संख्याएं हैं, तो उत्तर हमेशा सरणी में सबसे बड़ी संख्या होगी, यह मानते हुए कि हम खाली उपसरणी की अनुमति नहीं दे रहे हैं।

-यदि किसी सरणी में केवल सकारात्मक संख्याएं हैं, तो उत्तर हमेशा संपूर्ण सरणी को जोड़ना होगा।

-यदि आपके पास सकारात्मक और नकारात्मक दोनों संख्याओं की एक सरणी है, तो आप चरण दर चरण सरणी को पार कर सकते हैं। यदि किसी भी बिंदु पर आप जो संख्या देख रहे हैं वह उससे पहले आई सभी संख्याओं के योग से बड़ी है, तो समाधान में पिछली कोई भी संख्या शामिल नहीं हो सकती है। इस प्रकार, आप अब तक प्राप्त अधिकतम राशि का ध्यान रखते हुए, वर्तमान संख्या से एक नई राशि शुरू करते हैं।

maxSubArray(nums):
    # avoiding type errors or index out of bounds errors
    if nums is None or len(nums) == 0:
        return 0


    max_sum = nums[0]  # max sum can't be smaller than any given element
    curr_sum = 0

    # Kadane's algorithm
    for num in nums:
        curr_sum = max(num, curr_sum   num)
        max_sum = max(curr_sum, max_sum)
    return max_sum

इस एल्गोरिदम के बारे में मुझे जो पसंद है वह यह है कि इसे कई अन्य समस्याओं पर भी लागू किया जा सकता है। इन लीटकोड समस्याओं को हल करने के लिए इसे अपनाने का प्रयास करें:

एक और शून्य
अधिकतम योग परिपत्र उपसरणी
न्यूनतम आकार उपसरणी योग
अधिकतम आरोही उपसरणी योग
अधिकतम उत्पाद उपसरणी
सतत उपसरणी योग
अधिकतम वैकल्पिक योग उपसरणी (प्रीमियम)
आयत का अधिकतम योग K से बड़ा नहीं