Comme nous avons parlé de différents algorithmes de tri, nous allons aujourd'hui découvrir l'algorithme de tri par sélection. Un algorithme de tri qui permet le nombre minimum d'échanges possible dans un environnement à mémoire limitée.

Table des matières

1. Introduction
2. Qu'est-ce que l'algorithme de tri par sélection ?
3. Comment fonctionne le tri par sélection ?
   • Complexité temporelle
   • Complexité spatiale
4. Implémentation en JavaScript
5. Résoudre les problèmes de LeetCode
6. Conclusion

Introduction

Le tri par sélection est un algorithme de tri simple mais efficace qui fonctionne en sélectionnant à plusieurs reprises l'élément le plus petit (ou le plus grand) de la partie non triée de la liste et en le déplaçant au début (ou à la fin) de la partie triée. Ce processus est répété jusqu'à ce que la liste entière soit triée. Dans cet article, nous approfondirons les détails de l'algorithme de tri par sélection, son implémentation en JavaScript et ses applications pour résoudre des problèmes du monde réel.

Qu’est-ce que l’algorithme de tri par sélection ?

L'algorithme de tri par sélection est un algorithme de tri par comparaison sur place. Il divise la liste d'entrée en deux parties :

1. La partie triée à l'extrémité gauche
2. La partie non triée à l'extrémité droite

L'algorithme sélectionne à plusieurs reprises le plus petit élément de la partie non triée et l'échange avec l'élément non trié le plus à gauche, déplaçant la limite entre les parties triées et non triées d'un élément vers la droite.

Comment fonctionne le tri par sélection ?

Parcourons un exemple utilisant le tableau [64, 25, 12, 22, 11] :

1. Tableau initial : [64, 25, 12, 22, 11]

• Part triée : []
• Part non triée : [64, 25, 12, 22, 11]

1. Premier passage :

• Trouver le minimum en portion non triée : 11
• Échanger 11 avec le premier élément non trié (64)
• Résultat : [11, 25, 12, 22, 64]
• Part triée : [11]
• Part non triée : [25, 12, 22, 64]

1. Deuxième passage :

• Trouver minimum en portion non triée : 12
• Échanger 12 avec le premier élément non trié (25)
• Résultat : [11, 12, 25, 22, 64]
• Part triée : [11, 12]
• Part non triée : [25, 22, 64]

1. Troisième passage :

• Trouver le minimum en portion non triée : 22
• Échanger 22 avec le premier élément non trié (25)
• Résultat : [11, 12, 22, 25, 64]
• Part triée : [11, 12, 22]
• Part non triée : [25, 64]

1. Quatrième passage :

• Trouver minimum en portion non triée : 25
• 25 est déjà dans la bonne position
• Résultat : [11, 12, 22, 25, 64]
• Part triée : [11, 12, 22, 25]
• Part non triée : [64]

1. Réussite finale :
   • Il ne reste qu'un élément, il est automatiquement à la bonne position
   • Résultat final : [11, 12, 22, 25, 64]

Le tableau est maintenant entièrement trié.

Complexité temporelle

Le tri par sélection a une complexité temporelle de O(n^2) dans tous les cas (meilleur, moyen et pire), où n est le nombre d'éléments dans le tableau. En effet :

• La boucle externe s'exécute n-1 fois
• Pour chaque itération de la boucle externe, la boucle interne s'exécute n-i-1 fois (où i est l'itération actuelle de la boucle externe)

Cela donne environ (n^2)/2 comparaisons et n échanges, ce qui se simplifie en O(n^2).

En raison de cette complexité temporelle quadratique, le tri par sélection n'est pas efficace pour les grands ensembles de données. Cependant, sa simplicité et le fait qu'il effectue le minimum de swaps possible peuvent le rendre utile dans certaines situations, notamment lorsque la mémoire auxiliaire est limitée.

Complexité spatiale

Selection Sort a une complexité spatiale de O(1) car il trie le tableau sur place. Il nécessite uniquement une quantité constante d'espace mémoire supplémentaire, quelle que soit la taille d'entrée. Cela le rend efficace en termes de mémoire, ce qui peut être avantageux dans les environnements où la mémoire est limitée.

Implémentation en JavaScript

Voici une implémentation JavaScript de l'algorithme de tri par sélection :

function selectionSort(arr) {
  const n = arr.length;

  for (let i = 0; i 


Décomposons le code :

Nous définissons une fonction SelectionSort qui prend un tableau en entrée.
Nous parcourons le tableau avec la boucle externe (i), qui représente la limite entre les parties triées et non triées.
Pour chaque itération, nous supposons que le premier élément non trié est le minimum et stockons son index.
Nous utilisons ensuite une boucle interne (j) pour trouver l'élément minimum réel dans la partie non triée.
Si nous trouvons un élément plus petit, nous mettons à jour minIndex.
Après avoir trouvé le minimum, on l'échange avec le premier élément non trié si nécessaire.
Nous répétons ce processus jusqu'à ce que l'ensemble du tableau soit trié.

  
  
  Résoudre les problèmes de LeetCode


Résolvons un problème d'algorithme leetcode en utilisant l'algorithme de tri par sélection. Allons-nous?

  
  
  Problème : trier un tableau [Moyen]


Problème : Étant donné un tableau de nombres entiers, triez le tableau par ordre croissant et renvoyez-le. Vous devez résoudre le problème sans utiliser de fonctions intégrées dans une complexité temporelle O(nlog(n)) et avec la plus petite complexité spatiale possible.

Approche : : Pour résoudre ce problème, nous pouvons appliquer directement l'algorithme de tri par sélection. Cela implique de parcourir le tableau, de trouver le plus petit élément dans la partie non triée et de l'échanger avec le premier élément non trié. Nous répétons ce processus jusqu'à ce que l'ensemble du tableau soit trié.

Solution:

// This function sorts an array of integers in ascending order using the Selection Sort algorithm.
const sortArray = function (nums) {
  // Get the length of the input array.
  const n = nums.length;

  // Iterate through the array, starting from the first element.
  for (let i = 0; i 


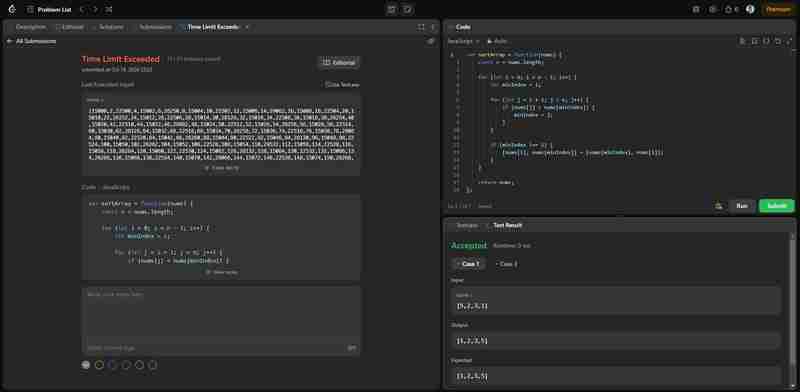
Cette solution applique directement l'algorithme de tri par sélection que nous avons implémenté précédemment. Bien qu'elle résout correctement le problème, il convient de noter que cette solution peut dépasser la limite de temps pour les entrées volumineuses sur LeetCode en raison de la complexité temporelle O(n^2) du tri par sélection. L'image ci-dessous montre que la solution est correcte mais pas efficace.



  
  
  Conclusion


En conclusion, Selection Sort est un algorithme de tri simple et intuitif qui constitue une excellente introduction au monde des techniques de tri. Sa simplicité le rend facile à comprendre et à mettre en œuvre, ce qui en fait un outil d'apprentissage précieux pour les débutants. Cependant, en raison de sa complexité temporelle quadratique O(n^2), il n'est pas efficace pour les grands ensembles de données. Pour les ensembles de données plus volumineux ou les applications critiques en termes de performances, des algorithmes plus efficaces tels que QuickSort, MergeSort ou des fonctions de tri intégrées sont préférés.


  
  
  Restez à jour et connecté


Pour vous assurer de ne manquer aucune partie de cette série et pour me contacter pour plus de détails

discussions sur le Développement Logiciel (Web, Serveur, Mobile ou Scraping/Automatisation), les données

structures et algorithmes, et d'autres sujets technologiques passionnants, suivez-moi sur :



    
      

        
    
  

    

La grande solution ?Suivez

    

      Ingénieur logiciel | Rédacteur technique | Développeur Backend, Web & Mobile ? | Passionné par la création de solutions logicielles efficaces et évolutives. #connectons-nous ?
    
  

• GitHub
• Linkedin
• X (Twitter)

Restez à l'écoute et bon codage ?‍??