Introducción 1

El proceso en el que una función se llama a sí misma se llama recursividad y el
la función correspondiente se llama función recursiva.
Dado que la programación informática es una aplicación fundamental de las matemáticas,
Primero intentemos comprender el razonamiento matemático detrás de la recursividad.
En general, todos conocemos el concepto de funciones. En pocas palabras, las funciones son
ecuaciones matemáticas que producen una salida al proporcionar una entrada. Por ejemplo:
Supongamos que la función F(x) es una función definida por: F(x) = x^2 4
Podemos escribir el código Java para esta función como:

público estático int F(int x){
devolver (x * x 4);
}

Ahora, podemos pasar diferentes valores de x a esta función y recibir nuestra salida
respectivamente.
Antes de pasar a la recursividad, intentemos comprender otra matemática
concepto conocido como Principio de Inducción Matemática (PMI).

El Principio de Inducción Matemática (PMI) es una técnica para demostrar un enunciado, un
fórmula o teorema que se afirma sobre un conjunto de números naturales. Tiene el
siguientes tres pasos:
1.** Paso del caso trivial*: En este paso, probaremos la afirmación deseada para
un caso base como n = 0 o n = 1.
2.* Paso de suposición**: En este paso, asumiremos que la declaración deseada
es válido para n = k.

1. Para probar el paso: A partir de los resultados del paso de suposición, demostraremos que, n = k 1 también es cierto para la ecuación deseada siempre que n = k sea verdadero.

Por ejemplo: demostremos usando el principio de inducción matemática que:
S(norte): 1 2 3 ... norte = (norte * (norte 1))/2
(La suma de los primeros N números naturales)
Prueba:
Paso 1: Para N = 1, S(1) = 1 es verdadero.
Paso 2: Suponga que la afirmación dada es verdadera para N = k, es decir,
1 2 3 .... k = (k * (k 1))/2
Paso 3: Demostremos la afirmación para N = k 1 usando el paso 2.

Para demostrar: 1 2 3 ... (k 1) = ((k 1)*(k 2))/2
Prueba:

Añadiendo (k 1) tanto a LHS como a RHS en el resultado obtenido en el paso 2:
1 2 3 ... (k 1) = (k*(k 1))/2 (k 1)

Ahora, tomando (k 1) común del lado derecho:
1 2 3 ... (k 1) = (k 1)*((k 2)/2)

Según la afirmación que estamos intentando probar:
1 2 3 ... (k 1) = ((k 1)*(k 2))/2
Por tanto, demostrado.

Trabajo de recursividad

Podemos definir los pasos del enfoque recursivo resumiendo los tres anteriores
pasos:
● Caso base: una función recursiva debe tener una condición final en la que
el proceso dejará de llamarse a sí mismo. Un caso así se conoce como caso base. Sin un caso base, seguirá llamándose a sí mismo y se quedará atascado en un
bucle infinito. Pronto, se excederá la profundidad de recursividad* y arrojará
un error.
● Llamada recursiva: la función recursiva se invocará a sí misma en una versión más pequeña
del problema principal. Debemos tener cuidado al escribir este paso tal como está
crucial para determinar correctamente cuál es su problema más pequeño.
● Cálculo pequeño: generalmente, realizamos un paso de cálculo en cada recursivo
llamar. Podemos realizar este paso de cálculo antes o después de la llamada recursiva
dependiendo de la naturaleza del problema.

Nota: La recursión utiliza una pila incorporada que almacena llamadas recursivas. Por lo tanto, el
El número de llamadas recursivas debe ser lo más pequeño posible para evitar el desbordamiento de la memoria. Si
el número de llamadas recursivas excede la cantidad máxima permitida, el
**Se excederá la profundidad de recursividad**.
Ahora, veamos cómo resolver algunos problemas comunes usando Recursion

Enunciado del problema: encontrar el factorial de un número

Enfoque: descubrir los tres pasos del PMI y luego relacionarlos usando
recursividad

1. Paso de inducción: Calcular el factorial de un número n - F(n) Hipótesis de Inducción: Ya hemos obtenido el factorial de n-1 - F(n-1)
2. Expresando F(n) en términos de F(n-1): F(n)=n*F(n-1). Así obtenemos

hecho int estático público (int n){
int ans = hecho(n-1); #Paso de asunción
devolver ans * n; #Resolver el problema desde el paso de suposición
}

1. El código aún no está completo. La parte que falta es el caso base. ahora lo haremos Realice un ensayo para encontrar el caso en el que la recursividad debe detenerse. Considere n = 5:

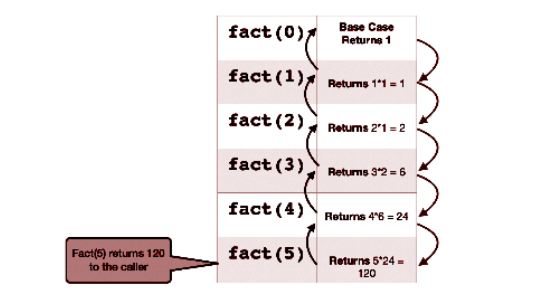
Como podemos ver arriba, ya sabemos la respuesta de n = 0, que es 1. Así que
mantenga esto como nuestro caso base. Por lo tanto, el código ahora se convierte en:

público estático int factorial(int n){
if (n == 0) // caso base
devolver 1;
demás
devolver n*factorial(n-1); // caso recursivo
}