k-Regresión de vecinos más cercanos

La regresión de k-vecinos más cercanos (k-NN) es un método no paramétrico que predice el valor de salida en función del promedio (o promedio ponderado) de los k puntos de datos de entrenamiento más cercanos en el espacio de características. Este enfoque puede modelar eficazmente relaciones complejas en datos sin asumir una forma funcional específica.

El método de regresión k-NN se puede resumir de la siguiente manera:

1. Métrica de distancia: el algoritmo utiliza una métrica de distancia (comúnmente distancia euclidiana) para determinar la "cercanía" de los puntos de datos.
2. k Vecinos: El parámetro k especifica cuántos vecinos más cercanos se deben considerar al realizar predicciones.
3. Predicción: El valor predicho para un nuevo punto de datos es el promedio de los valores de sus k vecinos más cercanos.

Conceptos clave

1. No paramétrico: a diferencia de los modelos paramétricos, k-NN no asume una forma específica para la relación subyacente entre las características de entrada y la variable objetivo. Esto lo hace flexible a la hora de capturar patrones complejos.

2. Cálculo de distancia: La elección de la métrica de distancia puede afectar significativamente el rendimiento del modelo. Las métricas comunes incluyen distancias euclidianas, de Manhattan y de Minkowski.

3. Elección de k: El número de vecinos (k) se puede elegir en función de la validación cruzada. Una k pequeña puede provocar un sobreajuste, mientras que una k grande puede suavizar demasiado la predicción, lo que podría provocar un desajuste.

Ejemplo de regresión de k-vecinos más cercanos

Este ejemplo demuestra cómo utilizar la regresión k-NN con características polinomiales para modelar relaciones complejas mientras se aprovecha la naturaleza no paramétrica de k-NN.

Ejemplo de código Python

1. Importar bibliotecas

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, r2_score

Este bloque importa las bibliotecas necesarias para la manipulación de datos, el trazado y el aprendizaje automático.

2. Generar datos de muestra

np.random.seed(42)  # For reproducibility
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = 3 * X.ravel()   np.sin(2 * X.ravel()) * 5   np.random.normal(0, 1, 100)

Este bloque genera datos de muestra que representan una relación con algo de ruido, simulando variaciones de datos del mundo real.

3. Dividir el conjunto de datos

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Este bloque divide el conjunto de datos en conjuntos de entrenamiento y prueba para la evaluación del modelo.

4. Crear entidades polinómicas

degree = 3  # Change this value for different polynomial degrees
poly = PolynomialFeatures(degree=degree)
X_poly_train = poly.fit_transform(X_train)
X_poly_test = poly.transform(X_test)

Este bloque genera características polinómicas a partir de los conjuntos de datos de entrenamiento y prueba, lo que permite que el modelo capture relaciones no lineales.

5. Cree y entrene el modelo de regresión k-NN

k = 5  # Number of neighbors
knn_model = KNeighborsRegressor(n_neighbors=k)
knn_model.fit(X_poly_train, y_train)

Este bloque inicializa el modelo de regresión k-NN y lo entrena utilizando las características polinómicas derivadas del conjunto de datos de entrenamiento.

6. Hacer predicciones

y_pred = knn_model.predict(X_poly_test)

Este bloque utiliza el modelo entrenado para hacer predicciones en el conjunto de prueba.

7. Trazar los resultados

plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', alpha=0.5, label='Data Points')
X_grid = np.linspace(0, 10, 1000).reshape(-1, 1)
X_poly_grid = poly.transform(X_grid)
y_grid = knn_model.predict(X_poly_grid)
plt.plot(X_grid, y_grid, color='red', linewidth=2, label=f'k-NN Regression (k={k}, Degree {degree})')
plt.title(f'k-NN Regression (Polynomial Degree {degree})')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()

Este bloque crea un diagrama de dispersión de los puntos de datos reales versus los valores predichos del modelo de regresión k-NN, visualizando la curva ajustada.

Salida con k = 1:

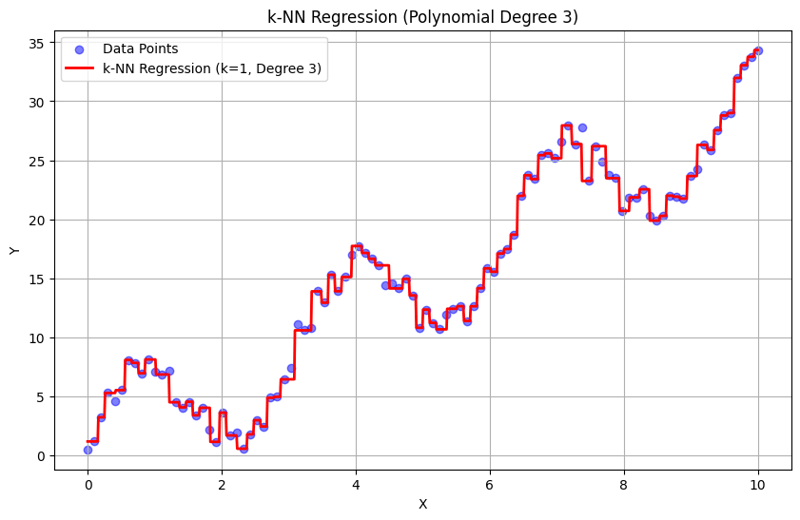
Salida con k = 10:

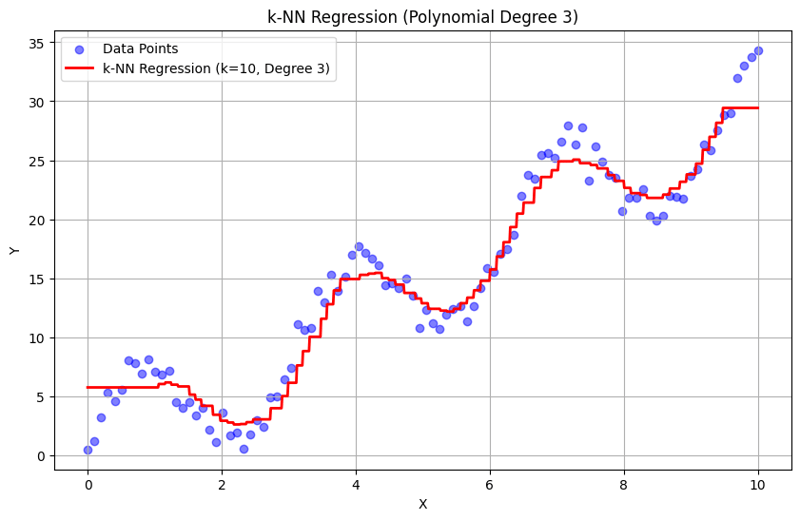
Este enfoque estructurado demuestra cómo implementar y evaluar la regresión de k-vecinos más cercanos con características polinómicas. Al capturar patrones locales mediante el promedio de las respuestas de los vecinos cercanos, la regresión k-NN modela de manera efectiva relaciones complejas en los datos y, al mismo tiempo, proporciona una implementación sencilla. La elección de k y el grado del polinomio influye significativamente en el rendimiento y la flexibilidad del modelo para capturar las tendencias subyacentes.