El problema del subarreglo máximo y su historia.

A finales de la década de 1970, el matemático sueco Ulf Grenander había estado discutiendo un problema: ¿cómo se puede analizar una matriz 2D de datos de imágenes de manera más eficiente que la fuerza bruta? En aquel entonces, las computadoras eran lentas y las imágenes eran grandes en relación con la RAM. Para exacerbar las cosas, en el peor de los casos, la fuerza bruta tomó O(n^6) tiempo (complejidad de tiempo sextico).

Primero, Grenandier simplificó la pregunta: dada una matriz unidimensional de números, ¿cómo encontrarías de manera más eficiente la submatriz contigua con la suma más grande?

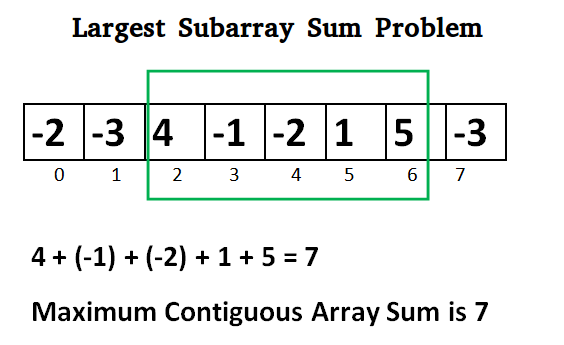
Fuerza bruta: un enfoque ingenuo con complejidad del tiempo cúbico

Fuerza bruta, tomaría la mitad de tiempo analizar una matriz 1D que una matriz 2D, por lo que O(n^3) para examinar todas las combinaciones posibles (complejidad del tiempo cúbico).

def max_subarray_brute_force(arr):
    max_sum = arr[0] # assumes arr has a length

    # iterate over all possible subarrays
    for i in range(len(arr)):
        for j in range(i, len(arr)):
            current_sum = 0
            # sum the elements of the subarray arr[i:j 1]
            for k in range(i, j   1):
                current_sum  = arr[k]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

print(max_subarray_brute_force([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

Optimización O(n²) de Grenander: un paso adelante

Granander lo mejoró a la solución O(n^2). No pude encontrar su código en mi investigación, pero supongo que simplemente se deshizo del bucle más interno que suma todos los números entre los dos índices. En su lugar, podemos mantener una suma acumulada mientras iteramos sobre el subarreglo, reduciendo así el número de bucles de tres a dos.

def max_subarray_optimized(arr):
    max_sum = arr[0]  # assumes arr has a length

    # iterate over all possible starting points of the subarray
    for i in range(len(arr)):
        current_sum = 0
        # sum the elements of the subarray starting from arr[i]
        for j in range(i, len(arr)):
            current_sum  = arr[j]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

Divide y vencerás de Shamos: dividir el problema para O(n log n)

Granander le mostró el problema al informático Michael Shamos. Shamos lo pensó durante una noche y se le ocurrió un método de divide y vencerás que es O(n log n).

Es bastante inteligente. La idea es dividir la matriz en dos mitades y luego encontrar de forma recursiva la suma máxima del subarreglo para cada mitad, así como el subarreglo que cruza el punto medio.

def max_crossing_sum(arr, left, mid, right):
    # left of mid
    left_sum = float('-inf')
    current_sum = 0
    for i in range(mid, left - 1, -1):
        current_sum  = arr[i]
        left_sum = max(left_sum, current_sum)

    # right of mid
    right_sum = float('inf')
    current_sum = 0
    for i in range(mid   1, right   1):
        current_sum  = arr[i]
        right_sum = max(right_sum, current_sum)

    # sum of elements on the left and right of mid, which is the maximum sum that crosses the midpoint
    return left_sum   right_sum

def max_subarray_divide_and_conquer(arr, left, right):
    # base case: only one element
    if left == right:
        return arr[left]

    # find the midpoint
    mid = (left   right) // 2

    # recursively find the maximum subarray sum for the left and right halves
    left_sum = max_subarray_divide_and_conquer(arr, left, mid)
    right_sum = max_subarray_divide_and_conquer(arr, mid   1, right)
    cross_sum = max_crossing_sum(arr, left, mid, right)

    # return the maximum of the three possible cases
    return max(left_sum, right_sum, cross_sum)

def max_subarray(arr):
    return max_subarray_divide_and_conquer(arr, 0, len(arr) - 1)


print(max_subarray([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

Esto reduce la complejidad del tiempo a O(nlogn) porque primero la matriz se divide en dos mitades (O(logn)) y luego, para encontrar el subarreglo de cruce máximo, se requiere O(n)

Algoritmo de Kadane: la elegante solución O(n)

El estadístico Jay Kadane examinó el código e inmediatamente identificó que la solución de Shamos no utilizó la restricción de contigüidad como parte de la solución.

Esto es lo que se dio cuenta

-Si una matriz solo tiene números negativos, entonces la respuesta siempre será el número más grande de la matriz, asumiendo que no permitimos subarreglos vacíos.

-Si un array solo tiene números positivos, la respuesta siempre será sumar todo el array.

-Si tiene una matriz de números positivos y negativos, puede recorrer la matriz paso a paso. Si en algún momento el número que estás viendo es mayor que la suma de todos los números anteriores, la solución no puede incluir ninguno de los números anteriores. Por lo tanto, comienza una nueva suma a partir del número actual, mientras realiza un seguimiento de la suma máxima encontrada hasta el momento.

maxSubArray(nums):
    # avoiding type errors or index out of bounds errors
    if nums is None or len(nums) == 0:
        return 0


    max_sum = nums[0]  # max sum can't be smaller than any given element
    curr_sum = 0

    # Kadane's algorithm
    for num in nums:
        curr_sum = max(num, curr_sum   num)
        max_sum = max(curr_sum, max_sum)
    return max_sum

Lo que me encanta de este algoritmo es que se puede aplicar a muchos otros problemas. Intente adaptarlo para resolver estos problemas de LeetCode:

Unos y ceros
Submatriz circular de suma máxima
Suma de submatriz de tamaño mínimo
Suma máxima de subarreglo ascendente
Subconjunto máximo de productos
Suma de subarreglo continuo
Submatriz de suma alterna máxima (premium)
Suma máxima de rectángulo no mayor que K