Como hemos estado hablando sobre diferentes algoritmos de clasificación, hoy aprenderemos sobre el algoritmo de clasificación por selección. Un algoritmo de clasificación que permite la cantidad mínima posible de intercambios en un entorno con memoria limitada.

Tabla de contenido

1. Introducción
2. ¿Qué es el algoritmo de clasificación por selección?
3. ¿Cómo funciona la clasificación por selección?
   • Complejidad del tiempo
   • Complejidad espacial
4. Implementación en JavaScript
5. Resolviendo problemas de LeetCode
6. Conclusión

Introducción

La clasificación por selección es un algoritmo de clasificación simple pero efectivo que funciona seleccionando repetidamente el elemento más pequeño (o más grande) de la parte no ordenada de la lista y moviéndolo al principio (o al final) de la parte ordenada. Este proceso se repite hasta que se ordena toda la lista. En este artículo, profundizaremos en los detalles del algoritmo de ordenación por selección, su implementación en JavaScript y sus aplicaciones para resolver problemas del mundo real.

¿Qué es el algoritmo de clasificación por selección?

El algoritmo de clasificación por selección es un algoritmo de clasificación por comparación in situ. Divide la lista de entrada en dos partes:

1. La parte ordenada en el extremo izquierdo
2. La parte sin clasificar en el extremo derecho

El algoritmo selecciona repetidamente el elemento más pequeño de la parte sin clasificar y lo intercambia con el elemento sin clasificar más a la izquierda, moviendo el límite entre las partes ordenadas y sin clasificar un elemento hacia la derecha.

¿Cómo funciona la clasificación por selección?

Veamos un ejemplo usando la matriz [64, 25, 12, 22, 11]:

1. Matriz inicial: [64, 25, 12, 22, 11]

• Porción ordenada: []
• Porción sin clasificar: [64, 25, 12, 22, 11]

1. Primer pase:

• Encontrar mínimo en la porción sin clasificar: 11
• Intercambiar 11 con el primer elemento sin clasificar (64)
• Resultado: [11, 25, 12, 22, 64]
• Porción ordenada: [11]
• Porción sin clasificar: [25, 12, 22, 64]

1. Segundo pase:

• Encontrar mínimo en la porción sin clasificar: 12
• Intercambiar 12 con el primer elemento sin clasificar (25)
• Resultado: [11, 12, 25, 22, 64]
• Porción ordenada: [11, 12]
• Porción sin clasificar: [25, 22, 64]

1. Tercer pase:

• Encontrar mínimo en la porción sin clasificar: 22
• Intercambiar 22 con el primer elemento sin clasificar (25)
• Resultado: [11, 12, 22, 25, 64]
• Porción ordenada: [11, 12, 22]
• Porción sin clasificar: [25, 64]

1. Cuarto pase:

• Encontrar mínimo en la porción sin clasificar: 25
• 25 ya está en la posición correcta
• Resultado: [11, 12, 22, 25, 64]
• Porción ordenada: [11, 12, 22, 25]
• Porción sin clasificar: [64]

1. Pase final:
   • Solo queda un elemento, automáticamente está en la posición correcta
   • Resultado final: [11, 12, 22, 25, 64]

La matriz ahora está completamente ordenada.

Complejidad del tiempo

La clasificación por selección tiene una complejidad temporal de O(n^2) en todos los casos (mejor, promedio y peor), donde n es el número de elementos de la matriz. Esto se debe a que:

• El bucle exterior se ejecuta n-1 veces
• Para cada iteración del bucle externo, el bucle interno se ejecuta n-i-1 veces (donde i es la iteración actual del bucle externo)

Esto da como resultado aproximadamente (n^2)/2 comparaciones y n intercambios, lo que se simplifica a O(n^2).

Debido a esta complejidad de tiempo cuadrático, la clasificación por selección no es eficiente para conjuntos de datos grandes. Sin embargo, su simplicidad y el hecho de que realiza el mínimo número posible de intercambios puede hacerlo útil en determinadas situaciones, especialmente cuando la memoria auxiliar es limitada.

Complejidad espacial

La ordenación por selección tiene una complejidad espacial de O(1) porque ordena la matriz en el lugar. Solo requiere una cantidad constante de espacio de memoria adicional independientemente del tamaño de entrada. Esto lo hace eficiente en cuanto a memoria, lo que puede resultar ventajoso en entornos con memoria limitada.

Implementación en JavaScript

Aquí hay una implementación de JavaScript del algoritmo de ordenación por selección:

function selectionSort(arr) {
  const n = arr.length;

  for (let i = 0; i 


Desglosemos el código:

Definimos una función de selección que toma una matriz como entrada.
Repetimos la matriz con el bucle externo (i), que representa el límite entre las partes ordenadas y no ordenadas.
Para cada iteración, asumimos que el primer elemento sin clasificar es el mínimo y almacenamos su índice.
Luego usamos un bucle interno (j) para encontrar el elemento mínimo real en la parte sin clasificar.
Si encontramos un elemento más pequeño, actualizamos minIndex.
Después de encontrar el mínimo, lo intercambiamos con el primer elemento sin clasificar si es necesario.
Repetimos este proceso hasta ordenar todo el arreglo.

  
  
  Resolviendo problemas de LeetCode


Resolvamos un problema de algoritmo leetcode utilizando un algoritmo de clasificación por selección. ¿Debemos?

  
  
  Problema: ordenar una matriz [mediana]


Problema: Dada una matriz de números enteros, ordene la matriz en orden ascendente y devuélvala. Debes resolver el problema sin utilizar ninguna función integrada en complejidad temporal O(nlog(n)) y con la menor complejidad espacial posible.

Enfoque:: Para resolver este problema, podemos aplicar directamente el algoritmo de clasificación por selección. Esto implica iterar a través de la matriz, encontrar el elemento más pequeño en la parte sin clasificar e intercambiarlo con el primer elemento sin clasificar. Repetimos este proceso hasta ordenar toda la matriz.

Solución:

// This function sorts an array of integers in ascending order using the Selection Sort algorithm.
const sortArray = function (nums) {
  // Get the length of the input array.
  const n = nums.length;

  // Iterate through the array, starting from the first element.
  for (let i = 0; i 


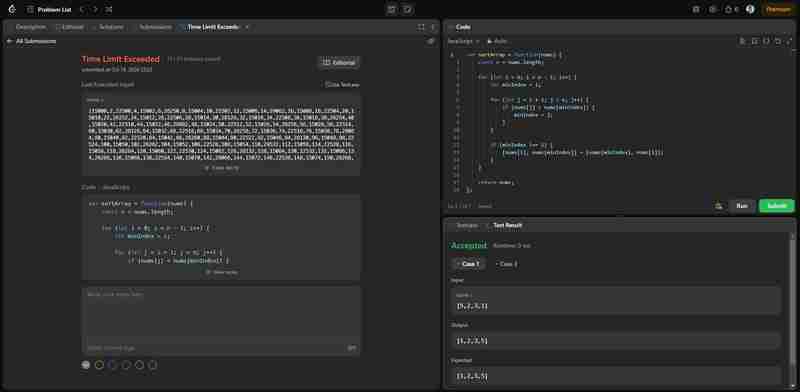
Esta solución aplica directamente el algoritmo de clasificación por selección que implementamos anteriormente. Si bien resuelve correctamente el problema, vale la pena señalar que esta solución puede exceder el límite de tiempo para entradas grandes en LeetCode debido a la complejidad temporal O(n^2) de Selection Sort. La siguiente imagen muestra que la solución es correcta pero no eficiente.



  
  
  Conclusión


En conclusión, Selection Sort es un algoritmo de clasificación simple e intuitivo que sirve como una excelente introducción al mundo de las técnicas de clasificación. Su simplicidad hace que sea fácil de entender e implementar, lo que la convierte en una valiosa herramienta de aprendizaje para principiantes. Sin embargo, debido a su complejidad temporal cuadrática O (n ^ 2), no es eficiente para conjuntos de datos grandes. Para conjuntos de datos más grandes o aplicaciones de rendimiento crítico, se prefieren algoritmos más eficientes como QuickSort, MergeSort o funciones de clasificación integradas.


  
  
  Manténgase actualizado y conectado


Para asegurarte de que no te pierdas ninguna parte de esta serie y para conectarte conmigo para obtener más detalles

debates sobre Desarrollo de Software (Web, Servidor, Móvil o Scraping/Automatización), datos

estructuras y algoritmos, y otros interesantes temas tecnológicos, sígueme en:



    
      

        
    
  

    

¿La gran solución?Seguir

    

      Ingeniero de software | Redactor técnico | ¿Desarrollador backend, web y móvil? | Apasionado por crear soluciones de software eficientes y escalables. #vamos a conectarnos?
    
  

• GitHub
• Linkedin
• X (Twitter)

Estén atentos y felices codificando ?‍??