Muchos problemas del mundo real se pueden resolver utilizando algoritmos gráficos. Los gráficos son útiles para modelar y resolver problemas del mundo real. Por ejemplo, el problema de encontrar el menor número de vuelos entre dos ciudades se puede modelar usando un gráfico, donde los vértices representan ciudades y los bordes representan los vuelos entre dos ciudades adyacentes, como se muestra en la Figura siguiente. El problema de encontrar el número mínimo de vuelos de conexión
entre dos ciudades se reduce a encontrar el camino más corto entre dos vértices de un gráfico.

El estudio de los problemas de grafos se conoce como teoría de grafos. La teoría de grafos fue fundada por Leonhard Euler en 1736, cuando introdujo la terminología de grafos para resolver el famoso problema de los Siete Puentes de Königsberg. La ciudad de Königsberg, Prusia (ahora Kaliningrado, Rusia), fue dividida por el río Pregel. Había dos islas en el río. La ciudad y las islas estaban conectadas por siete puentes, como se muestra en la Figura siguiente (a). La pregunta es: ¿se puede dar un paseo, cruzar cada puente exactamente una vez y volver al punto de partida? Euler demostró que no es posible.

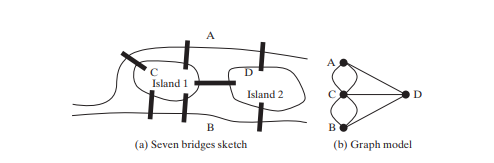
Para establecer una prueba, Euler primero abstrajo el mapa de la ciudad de Königsberg eliminando todas las calles, produciendo el boceto que se muestra en la Figura anterior (a). A continuación, reemplazó cada masa de tierra con un punto, llamado vértice o nodo, y cada puente con una línea, llamada borde, como se muestra en Figura arriba (b). Esta estructura con vértices y aristas se llama gráfico.

Mirando el gráfico, preguntamos si hay una ruta que comienza desde cualquier vértice, atraviesa todos los bordes exactamente una vez y regresa al vértice inicial. Euler demostró que para que exista tal camino, cada vértice debe tener un número par de aristas. Por tanto, el problema de los Siete Puentes de Königsberg no tiene solución.

Los problemas de gráficos a menudo se resuelven mediante algoritmos. Los algoritmos de gráficos tienen muchas aplicaciones en diversas áreas, como informática, matemáticas, biología, ingeniería, economía, genética y ciencias sociales.

Terminologías básicas de gráficos

Un gráfico consta de vértices y aristas que conectan los vértices. Este capítulo no asume que usted tenga conocimientos previos de teoría de grafos o matemáticas discretas. Usamos términos claros y simples para definir gráficos.

¿Qué es una gráfica? Un gráfico es una estructura matemática que representa relaciones entre entidades en el mundo real. Por ejemplo, el gráfico de la figura anterior representa los vuelos entre ciudades y el gráfico de la figura siguiente (b) representa los puentes entre masas de tierra.

Un gráfico consta de un conjunto no vacío de vértices (también conocidos como nodos o puntos) y un conjunto de aristas que conectan los vértices. Por conveniencia, definimos un gráfico como G = (V, E), donde V representa un conjunto de vértices y E representa un conjunto de aristas. Por ejemplo, V y E para el gráfico de la figura siguiente son los siguientes:

V = {"Seattle", "San Francisco", "Los Ángeles",
"Denver", "Kansas City", "Chicago", "Boston", "Nueva York",
"Atlanta", "Miami", "Dallas", "Houston"};

E = {{"Seattle", "San Francisco"},{"Seattle", "Chicago"},
{"Seattle", "Denver"}, {"San Francisco", "Denver"},
...
};

Un gráfico puede ser dirigido o no dirigido. En un gráfico dirigido, cada arista tiene una dirección, lo que indica que puedes moverte de un vértice al otro a través de la arista. Puede modelar relaciones padre/hijo usando un gráfico dirigido, donde un borde del vértice A al B indica que A es padre de B. La siguiente figura (a) muestra un gráfico dirigido.

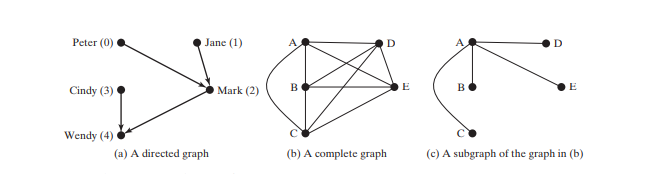
En un gráfico no dirigido, puedes moverte en ambas direcciones entre vértices. El gráfico de la figura siguiente no está dirigido.

Los bordes pueden estar ponderados o no ponderados. Por ejemplo, puede asignar un peso a cada borde en el gráfico de la figura anterior para indicar el tiempo de vuelo entre las dos ciudades.

Se dice que dos vértices en un gráfico son adyacentes si están conectados por el mismo borde. De manera similar, se dice que dos aristas son adyacentes si están conectadas al mismo vértice. Se dice que una arista en un gráfico que une dos vértices es incidente con ambos vértices. El grado de un vértice es el número de aristas incidentes en él.

Dos vértices se llaman vecinos si son adyacentes. De manera similar, dos aristas se denominan vecinas si son adyacentes.

Un bucle es una arista que vincula un vértice consigo mismo. Si dos vértices están conectados por dos o más aristas, estas aristas se denominan aristas paralelas. Un gráfico simple es aquel que no tiene bucles ni aristas paralelas. En un gráfico completo, cada dos pares de vértices están conectados, como se muestra en la Figura siguiente (b).

Un gráfico está conectado si existe una ruta entre dos vértices cualesquiera en el gráfico. Un subgrafo de un gráfico G es un gráfico cuyo conjunto de vértices es un subconjunto del de G y cuyo conjunto de aristas es un subconjunto del de G. Por ejemplo, el gráfico de la figura anterior (c) es un subgrafo del gráfico de la figura anterior (b).

Supongamos que el gráfico es conexo y no dirigido. Un ciclo es un camino cerrado que comienza desde un vértice y termina en el mismo vértice. Un gráfico conexo es un árbol si no tiene ciclos. Un árbol de expansión de un gráfico G es un subgrafo conexo de G y el subgrafo es un árbol que contiene todos los vértices en G.