Entonces, aquí está la historia: recientemente trabajé en una tarea escolar del profesor Zhuang que involucraba un algoritmo bastante interesante llamado Manta de Markov de Asociación Incremental (IAMB) . Ahora bien, no tengo experiencia en ciencia de datos o estadística, por lo que este es un territorio nuevo para mí, pero me encanta aprender algo nuevo. ¿El objetivo? Utilice IAMB para seleccionar funciones en un conjunto de datos y ver cómo afecta el rendimiento de un modelo de aprendizaje automático.

Repasaremos los conceptos básicos del algoritmo IAMB y los aplicaremos al Conjunto de datos sobre diabetes de los indios Pima de los conjuntos de datos de Jason Brownlee. Este conjunto de datos rastrea los datos de salud de las mujeres e incluye si tienen diabetes o no. Usaremos IAMB para determinar qué características (como el IMC o los niveles de glucosa) son más importantes para predecir la diabetes.

¿Qué es el algoritmo IAMB y por qué utilizarlo?

El algoritmo IAMB es como un amigo que te ayuda a limpiar una lista de sospechosos en un misterio: es un método de selección de funciones diseñado para seleccionar solo las variables que realmente importan para predecir tu objetivo. En este caso, el objetivo es si alguien tiene diabetes.

• Fase de avance: Agrega variables que estén fuertemente relacionadas con el objetivo.
• Fase de retroceso: elimina las variables que realmente no ayudan, asegurándote de que solo queden las más cruciales.

En términos más simples, IAMB nos ayuda a evitar el desorden en nuestro conjunto de datos al seleccionar solo las características más relevantes. Esto es especialmente útil cuando desea mantener las cosas simples, mejorar el rendimiento del modelo y acelerar el tiempo de entrenamiento.

Fuente: Algoritmos para el descubrimiento de mantas de Markov a gran escala

¿Qué es esto de Alfa y por qué es importante?

Aquí es donde entra alfa. En estadística, alfa (α) es el umbral que establecemos para decidir qué se considera "estadísticamente significativo". Como parte de las instrucciones dadas por el profesor, utilicé un alfa de 0,05, lo que significa que solo quiero conservar características que tengan menos del 5% de posibilidades de estar asociadas aleatoriamente con la variable objetivo. Entonces, si el valor p de una característica es menor que 0,05, significa que existe una asociación fuerte y estadísticamente significativa con nuestro objetivo.

Al utilizar este umbral alfa, nos centramos solo en las variables más significativas, ignorando aquellas que no pasan nuestra prueba de "significancia". Es como un filtro que mantiene las funciones más relevantes y elimina el ruido.

Práctica: uso de IAMB en el conjunto de datos sobre diabetes de los indios pima

Esta es la configuración: el conjunto de datos sobre diabetes de los indios Pima tiene características de salud (presión arterial, edad, niveles de insulina, etc.) y nuestro objetivo, Resultado (si alguien tiene diabetes).

Primero, cargamos los datos y los comprobamos:

import pandas as pd
# Load and preview the dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv'
column_names = ['Pregnancies', 'Glucose', 'BloodPressure', 'SkinThickness', 'Insulin', 'BMI', 'DiabetesPedigreeFunction', 'Age', 'Outcome']
data = pd.read_csv(url, names=column_names)
print(data.head())

Implementando IAMB con Alpha = 0.05

Aquí está nuestra versión actualizada del algoritmo IAMB. Estamos usando valores p para decidir qué funciones conservar, por lo que solo se seleccionan aquellas con valores p inferiores a nuestro alfa (0,05).

import pingouin as pg
def iamb(target, data, alpha=0.05):
    markov_blanket = set()
    # Forward Phase: Add features with a p-value  alpha
    for feature in list(markov_blanket):
        reduced_mb = markov_blanket - {feature}
        result = pg.partial_corr(data=data, x=feature, y=target, covar=reduced_mb)
        p_value = result.at[0, 'p-val']
        if p_value > alpha:
            markov_blanket.remove(feature)
    return list(markov_blanket)

# Apply the updated IAMB function on the Pima dataset
selected_features = iamb('Outcome', data, alpha=0.05)
print("Selected Features:", selected_features)

Cuando ejecuté esto, me dio una lista refinada de características que IAMB pensaba que estaban más estrechamente relacionadas con los resultados de la diabetes. Esta lista ayuda a reducir las variables que necesitamos para construir nuestro modelo.

Selected Features: ['BMI', 'DiabetesPedigreeFunction', 'Pregnancies', 'Glucose']

Prueba del impacto de las funciones seleccionadas por IAMB en el rendimiento del modelo

Una vez que tenemos nuestras funciones seleccionadas, la prueba real compara el rendimiento del modelo con todas las funciones versus funciones seleccionadas por IAMB. Para esto, elegí un modelo simple Gaussiano Naive Bayes porque es sencillo y funciona bien con las probabilidades (lo que se relaciona con toda la vibra bayesiana).

Aquí está el código para entrenar y probar el modelo:

from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score, f1_score, roc_auc_score

# Split data
X = data.drop('Outcome', axis=1)
y = data['Outcome']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Model with All Features
model_all = GaussianNB()
model_all.fit(X_train, y_train)
y_pred_all = model_all.predict(X_test)

# Model with IAMB-Selected Features
X_train_selected = X_train[selected_features]
X_test_selected = X_test[selected_features]

model_iamb = GaussianNB()
model_iamb.fit(X_train_selected, y_train)
y_pred_iamb = model_iamb.predict(X_test_selected)

# Evaluate models
results = {
    'Model': ['All Features', 'IAMB-Selected Features'],
    'Accuracy': [accuracy_score(y_test, y_pred_all), accuracy_score(y_test, y_pred_iamb)],
    'F1 Score': [f1_score(y_test, y_pred_all, average='weighted'), f1_score(y_test, y_pred_iamb, average='weighted')],
    'AUC-ROC': [roc_auc_score(y_test, y_pred_all), roc_auc_score(y_test, y_pred_iamb)]
}

results_df = pd.DataFrame(results)
display(results_df)

Resultados

Así es como se ve la comparación:

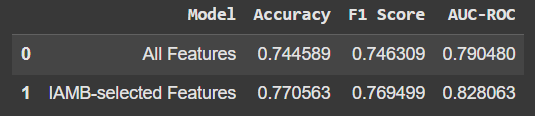
El uso solo de las funciones seleccionadas por IAMB dio un ligero aumento en la precisión y otras métricas. No es un gran salto, pero el hecho de que estemos obteniendo un mejor rendimiento con menos funciones es prometedor. Además, significa que nuestro modelo no se basa en "ruido" o datos irrelevantes.

Conclusiones clave

• IAMB es excelente para la selección de funciones: ayuda a limpiar nuestro conjunto de datos enfocándonos solo en lo que realmente importa para predecir nuestro objetivo.
• A menudo, menos es más: a veces, menos funciones nos dan mejores resultados, como vimos aquí con un pequeño aumento en la precisión del modelo.
• Aprender y experimentar es la parte divertida: Incluso sin una experiencia profunda en ciencia de datos, sumergirse en proyectos como este abre nuevas formas de comprender los datos y el aprendizaje automático.

¡Espero que esto brinde una introducción amigable a IAMB! Si tienes curiosidad, pruébalo: es una herramienta útil en la caja de herramientas de aprendizaje automático y es posible que veas algunas mejoras interesantes en tus propios proyectos.

Fuente: Algoritmos para el descubrimiento de mantas de Markov a gran escala