Das gewichtete Neun-Schwänze-Problem kann auf das gewichtete Kürzeste-Wege-Problem reduziert werden.
Abschnitt stellte das Neun-Schwänze-Problem vor und löste es mithilfe des BFS-Algorithmus. In diesem Abschnitt wird eine Variante des Problems vorgestellt und mithilfe des Kürzeste-Wege-Algorithmus gelöst.

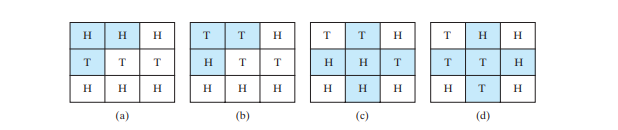
Das Neun-Schwänze-Problem besteht darin, die minimale Anzahl von Zügen zu finden, die dazu führen, dass alle Münzen nach unten zeigen. Bei jedem Zug werden eine Kopfmünze und ihre Nachbarn geworfen. Das gewichtete Problem mit neun Schwänzen weist jedem Zug die Anzahl der Würfe als Gewicht zu. Sie können beispielsweise die Münzen in Abbildung unten a in die in Abbildung unten b ändern, indem Sie die erste Münze in der ersten Reihe und ihre beiden Nachbarn umdrehen. Somit beträgt das Gewicht für diesen Zug 3. Sie können die Münzen in Abbildung unten c in Abbildung unten d ändern, indem Sie die mittlere Münze und ihre vier Nachbarn umdrehen. Das Gewicht für diesen Zug beträgt also 5.

Das gewichtete Neun-Schwanz-Problem kann auf die Suche nach einem kürzesten Weg von einem Startknoten zum Zielknoten in einem kantengewichteten Diagramm reduziert werden. Der Graph hat 512 Knoten. Erstellen Sie eine Kante vom Knoten v zum Knoten u, wenn eine Verschiebung vom Knoten u zum Knoten v erfolgt. Weisen Sie die Anzahl der Flips als Gewicht der Kante zu.

Erinnern Sie sich daran, dass wir im Abschnitt eine Klasse NineTailModel zur Modellierung des Neun-Schwänze-Problems definiert haben. Wir definieren jetzt eine neue Klasse mit dem Namen WeightedNineTailModel, die NineTailModel erweitert, wie in der Abbildung unten dargestellt.

Die Klasse NineTailModel erstellt einen Graph und erhält einen Baum, der am Zielknoten 511 verwurzelt ist. WeightedNineTailModel ist dasselbe wie NineTailModel, außer dass es einen WeightedGraph erstellt und einen ShortestPathTree erhält, der am Zielknoten verwurzelt ist 511. WeightedNineTailModel erweitert NineTailModel. Die Methode getEdges() findet alle Kanten im Diagramm. Die Methode getNumberOfFlips(int u, int v) gibt die Anzahl der Flips vom Knoten u zum Knoten v zurück. Die Methode getNumberOfFlips(int u) gibt die Anzahl der Flips vom Knoten u zum Zielknoten zurück.

Der folgende Code implementiert WeightedNineTailModel.

package demo;
import java.util.*;

public class WeightedNineTailModel extends NineTailModel {
    /** Construct a model */
    public WeightedNineTailModel() {
        // Create edges
        List edges = getEdges();

        // Create a graph
        WeightedGraph graph = new WeightedGraph(edges, NUMBER_OF_NODES);

        // Obtain a shortest path tree rooted at the target node
        tree = graph.getShortestPath(511);
    }

    /** Create all edges for the graph */
    private List getEdges() {
        // Store edges
        List edges = new ArrayList();

        for(int u = 0; u .ShortestPathTree)tree).getCost(u);
    }
}

WeightedNineTailModel erweitert NineTailModel, um einen WeightedGraph zu erstellen, um das gewichtete Neun-Schwänze-Problem zu modellieren (Zeilen 10–11). Für jeden Knoten u findet die Methode getEdges() einen umgedrehten Knoten v und weist die Anzahl der Umdrehungen als Gewicht für die Kante zu (v, u) (Zeile 30). Die Methode getNumberOfFlips(int u, int v) gibt die Anzahl der Flips vom Knoten u zum Knoten v zurück (Zeilen 38–47). Die Anzahl der Flips ist die Anzahl der verschiedenen Zellen zwischen dem
zwei Knoten (Zeile 44).

Das WeightedNineTailModel erhält einen ShortestPathTree, der auf dem Zielknoten 511 verwurzelt ist (Zeile 14). Beachten Sie, dass tree ein geschütztes Datenfeld ist, das in NineTailModel definiert ist und ShortestPathTree eine Unterklasse von Tree ist. Die in NineTailModel definierten Methoden verwenden die Eigenschaft tree.

Die Methode getNumberOfFlips(int u) (Zeilen 49–52) gibt die Anzahl der Flips vom Knoten u zum Zielknoten zurück, was den Kosten des Pfads vom Knoten entspricht u zum Zielknoten. Diese Kosten können durch Aufrufen der Methode getCost(u) ermittelt werden, die in der Klasse ShortestPathTree definiert ist (Zeile 51).

Der folgende Code gibt ein Programm an, das den Benutzer auffordert, einen Anfangsknoten einzugeben, und die Mindestanzahl von Flips anzeigt, um den Zielknoten zu erreichen.

package demo;

import java.util.Scanner;

public class WeightedNineTail {

    public static void main(String[] args) {
        // Prompt the user to enter nine coins' Hs and Ts
        System.out.print("Enter the initial nine coins Hs and Ts: ");
        Scanner input = new Scanner(System.in);
        String s = input.nextLine();
        char[] initialNode = s.toCharArray();

        WeightedNineTailModel model = new WeightedNineTailModel();
        java.util.List path = model.getShortestPath(NineTailModel.getIndex(initialNode));

        System.out.println("The steps to flip the coins are ");
        for (int i = 0; i 



Geben Sie zunächst neun Münzen Hs und Ts ein: HHHTTTHHH

Die Schritte zum Werfen der Münzen sind

HHH

TTT

HHH

HHH

THT

TTT

TTT

TTT

TTT

Die Anzahl der Flips beträgt 8

Das Programm fordert den Benutzer auf, einen Anfangsknoten mit neun Buchstaben mit einer Kombination aus Hs und Ts als Zeichenfolge in Zeile 8 einzugeben, erhält ein Array von Zeichen aus die Zeichenfolge (Zeile 9), erstellt ein Modell (Zeile 11), ermittelt den kürzesten Pfad vom Anfangsknoten zum Zielknoten (Zeilen 12–13), zeigt die Knoten im Pfad an (Zeilen 16–17), und ruft getNumberOfFlips auf, um die Anzahl der Flips zu erhalten, die zum Erreichen des Zielknotens erforderlich sind (Zeile 20).