k-Nächste-Nachbarn-Regression

k-Nearest Neighbors (k-NN)-Regression ist eine nichtparametrische Methode, die den Ausgabewert basierend auf dem Durchschnitt (oder gewichteten Durchschnitt) der k-nächsten Trainingsdatenpunkte im Merkmalsraum vorhersagt. Dieser Ansatz kann komplexe Beziehungen in Daten effektiv modellieren, ohne eine bestimmte funktionale Form anzunehmen.

Die k-NN-Regressionsmethode kann wie folgt zusammengefasst werden:

1. Distanzmetrik: Der Algorithmus verwendet eine Distanzmetrik (üblicherweise eine euklidische Distanz), um die „Nähe“ von Datenpunkten zu bestimmen.
2. k Nachbarn: Der Parameter k gibt an, wie viele nächste Nachbarn bei Vorhersagen berücksichtigt werden sollen.
3. Vorhersage: Der vorhergesagte Wert für einen neuen Datenpunkt ist der Durchschnitt der Werte seiner k nächsten Nachbarn.

Schlüsselkonzepte

1. Nicht parametrisch: Im Gegensatz zu parametrischen Modellen nimmt k-NN keine spezifische Form für die zugrunde liegende Beziehung zwischen den Eingabemerkmalen und der Zielvariablen an. Dies macht es flexibel bei der Erfassung komplexer Muster.

2. Entfernungsberechnung: Die Wahl der Entfernungsmetrik kann die Leistung des Modells erheblich beeinflussen. Zu den gängigen Maßen gehören Euklidische, Manhattan- und Minkowski-Entfernungen.

3. Auswahl von k: Die Anzahl der Nachbarn (k) kann basierend auf einer Kreuzvalidierung ausgewählt werden. Ein kleines k kann zu einer Überanpassung führen, während ein großes k die Vorhersage zu sehr glätten und möglicherweise zu einer Unteranpassung führen kann.

Beispiel für die k-Nächste-Nachbarn-Regression

Dieses Beispiel zeigt, wie man die k-NN-Regression mit Polynommerkmalen verwendet, um komplexe Beziehungen zu modellieren und gleichzeitig die nichtparametrische Natur von k-NN zu nutzen.

Beispiel für einen Python-Code

1. Bibliotheken importieren

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, r2_score

Dieser Block importiert die notwendigen Bibliotheken für Datenmanipulation, Darstellung und maschinelles Lernen.

2. Beispieldaten generieren

np.random.seed(42)  # For reproducibility
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = 3 * X.ravel()   np.sin(2 * X.ravel()) * 5   np.random.normal(0, 1, 100)

Dieser Block generiert Beispieldaten, die eine Beziehung mit etwas Rauschen darstellen und reale Datenvariationen simulieren.

3. Teilen Sie den Datensatz auf

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Dieser Block teilt den Datensatz in Trainings- und Testsätze zur Modellbewertung auf.

4. Polynom-Features erstellen

degree = 3  # Change this value for different polynomial degrees
poly = PolynomialFeatures(degree=degree)
X_poly_train = poly.fit_transform(X_train)
X_poly_test = poly.transform(X_test)

Dieser Block generiert Polynommerkmale aus den Trainings- und Testdatensätzen, sodass das Modell nichtlineare Beziehungen erfassen kann.

5. Erstellen und trainieren Sie das k-NN-Regressionsmodell

k = 5  # Number of neighbors
knn_model = KNeighborsRegressor(n_neighbors=k)
knn_model.fit(X_poly_train, y_train)

Dieser Block initialisiert das k-NN-Regressionsmodell und trainiert es mithilfe der aus dem Trainingsdatensatz abgeleiteten Polynommerkmale.

6. Vorhersagen treffen

y_pred = knn_model.predict(X_poly_test)

Dieser Block verwendet das trainierte Modell, um Vorhersagen zum Testsatz zu treffen.

7. Zeichnen Sie die Ergebnisse auf

plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', alpha=0.5, label='Data Points')
X_grid = np.linspace(0, 10, 1000).reshape(-1, 1)
X_poly_grid = poly.transform(X_grid)
y_grid = knn_model.predict(X_poly_grid)
plt.plot(X_grid, y_grid, color='red', linewidth=2, label=f'k-NN Regression (k={k}, Degree {degree})')
plt.title(f'k-NN Regression (Polynomial Degree {degree})')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()

Dieser Block erstellt ein Streudiagramm der tatsächlichen Datenpunkte im Vergleich zu den vorhergesagten Werten aus dem k-NN-Regressionsmodell und visualisiert die angepasste Kurve.

Ausgabe mit k = 1:

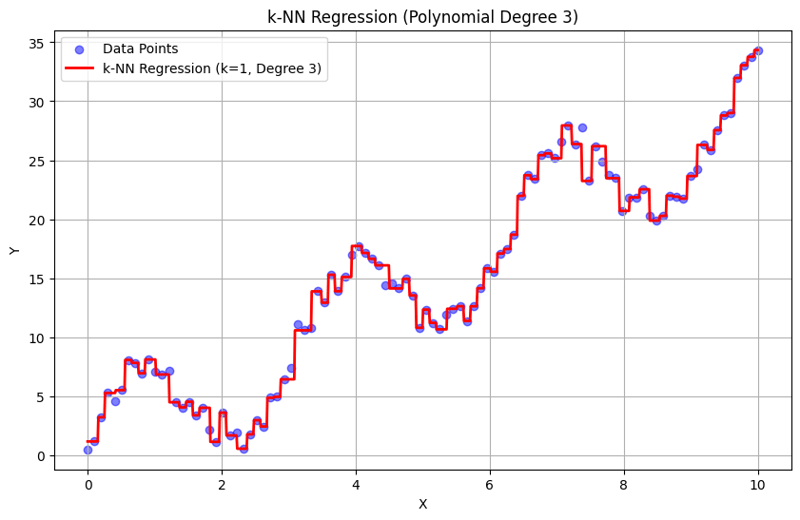
Ausgabe mit k = 10:

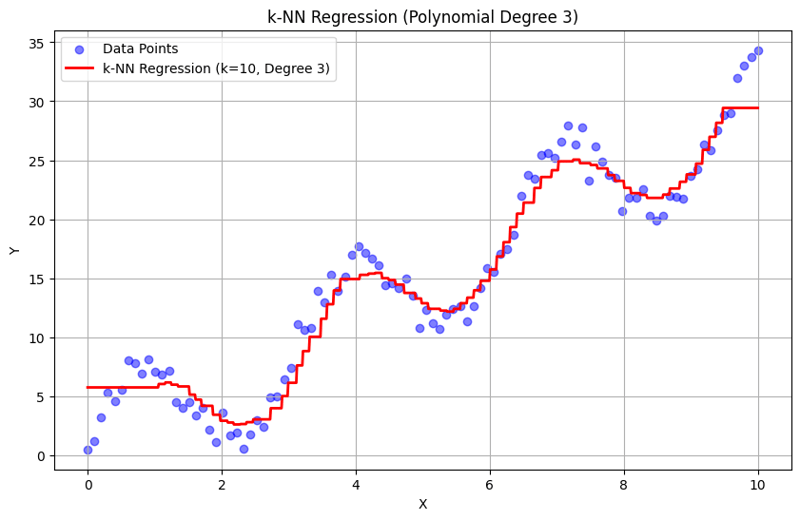
Dieser strukturierte Ansatz zeigt, wie die k-Nearest Neighbors-Regression mit Polynommerkmalen implementiert und ausgewertet wird. Durch die Erfassung lokaler Muster durch Mittelung der Antworten benachbarter Nachbarn modelliert die k-NN-Regression komplexe Beziehungen in Daten effektiv und bietet gleichzeitig eine unkomplizierte Implementierung. Die Wahl von k und Polynomgrad hat erheblichen Einfluss auf die Leistung und Flexibilität des Modells bei der Erfassung zugrunde liegender Trends.