Da wir über verschiedene Sortieralgorithmen gesprochen haben, lernen wir heute etwas über den Auswahlsortierungsalgorithmus. Ein Sortieralgorithmus, der die mögliche Mindestmenge an Auslagerungen in einer speicherbeschränkten Umgebung ermöglicht.

Inhaltsverzeichnis

1. Einführung
2. Was ist ein Auswahlsortierungsalgorithmus?
3. Wie funktioniert die Auswahlsortierung?
   • Zeitkomplexität
   • Weltraumkomplexität
4. Implementierung in JavaScript
5. LeetCode-Probleme lösen
6. Abschluss

Einführung

Selection Sort ist ein einfacher, aber effektiver Sortieralgorithmus, der durch wiederholtes Auswählen des kleinsten (oder größten) Elements aus dem unsortierten Teil der Liste und Verschieben an den Anfang (oder Ende) des sortierten Teils funktioniert. Dieser Vorgang wird wiederholt, bis die gesamte Liste sortiert ist. In diesem Artikel werden wir uns mit den Details des Auswahlsortierungsalgorithmus, seiner Implementierung in JavaScript und seinen Anwendungen bei der Lösung realer Probleme befassen.

Was ist ein Auswahlsortierungsalgorithmus?

Der Auswahlsortierungsalgorithmus ist ein Sortieralgorithmus für den direkten Vergleich. Es unterteilt die Eingabeliste in zwei Teile:

1. Der sortierte Teil am linken Ende
2. Der unsortierte Teil am rechten Ende

Der Algorithmus wählt wiederholt das kleinste Element aus dem unsortierten Teil aus und tauscht es mit dem am weitesten links stehenden unsortierten Element aus, wodurch die Grenze zwischen dem sortierten und dem unsortierten Teil um ein Element nach rechts verschoben wird.

Wie funktioniert die Auswahlsortierung?

Lassen Sie uns ein Beispiel mit dem Array [64, 25, 12, 22, 11] durchgehen:

1. Anfängliches Array: [64, 25, 12, 22, 11]

• Sortierter Teil: []
• Unsortierter Anteil: [64, 25, 12, 22, 11]

1. Erster Durchgang:

• Minimum im unsortierten Teil finden: 11
• Swap 11 mit dem ersten unsortierten Element (64)
• Ergebnis: [11, 25, 12, 22, 64]
• Sortierter Teil: [11]
• Unsortierter Anteil: [25, 12, 22, 64]

1. Zweiter Durchgang:

• Minimum im unsortierten Teil finden: 12
• Swap 12 mit dem ersten unsortierten Element (25)
• Ergebnis: [11, 12, 25, 22, 64]
• Sortierter Teil: [11, 12]
• Unsortierter Anteil: [25, 22, 64]

1. Dritter Durchgang:

• Minimum im unsortierten Teil finden: 22
• Swap 22 mit dem ersten unsortierten Element (25)
• Ergebnis: [11, 12, 22, 25, 64]
• Sortierter Teil: [11, 12, 22]
• Unsortierter Anteil: [25, 64]

1. Vierter Durchgang:

• Minimum im unsortierten Teil finden: 25
• 25 ist bereits an der richtigen Position
• Ergebnis: [11, 12, 22, 25, 64]
• Sortierter Teil: [11, 12, 22, 25]
• Unsortierter Anteil: [64]

1. Letzter Durchgang:
   • Nur noch ein Element übrig, es befindet sich automatisch an der richtigen Position
   • Endergebnis: [11, 12, 22, 25, 64]

Das Array ist jetzt vollständig sortiert.

Zeitkomplexität

Selection Sort hat in allen Fällen (beste, durchschnittliche und schlechteste) eine zeitliche Komplexität von O(n^2), wobei n die Anzahl der Elemente im Array ist. Das liegt daran:

• Die äußere Schleife läuft n-1 Mal
• Für jede Iteration der äußeren Schleife wird die innere Schleife n-i-1 Mal ausgeführt (wobei i die aktuelle Iteration der äußeren Schleife ist)

Dies führt zu ungefähr (n^2)/2 Vergleichen und n Swaps, was zu O(n^2) vereinfacht wird.

Aufgrund dieser quadratischen Zeitkomplexität ist die Auswahlsortierung für große Datensätze nicht effizient. Seine Einfachheit und die Tatsache, dass es die minimal mögliche Anzahl von Auslagerungen durchführt, können es jedoch in bestimmten Situationen nützlich machen, insbesondere wenn der Hilfsspeicher begrenzt ist.

Weltraumkomplexität

Selection Sort hat eine räumliche Komplexität von O(1), da es das Array direkt sortiert. Unabhängig von der Eingabegröße ist lediglich eine konstante Menge an zusätzlichem Speicherplatz erforderlich. Dies macht es speichereffizient, was in Umgebungen mit begrenztem Speicher von Vorteil sein kann.

Implementierung in JavaScript

Hier ist eine JavaScript-Implementierung des Auswahlsortierungsalgorithmus:

function selectionSort(arr) {
  const n = arr.length;

  for (let i = 0; i 


Lassen Sie uns den Code aufschlüsseln:

Wir definieren eine Funktion „selectionSort“, die ein Array als Eingabe verwendet.
Wir durchlaufen das Array mit der äußeren Schleife (i), die die Grenze zwischen den sortierten und unsortierten Teilen darstellt.
Für jede Iteration gehen wir davon aus, dass das erste unsortierte Element das Minimum ist und speichern seinen Index.
Wir verwenden dann eine innere Schleife (j), um das tatsächliche Mindestelement im unsortierten Teil zu finden.
Wenn wir ein kleineres Element finden, aktualisieren wir minIndex.
Nachdem wir das Minimum gefunden haben, tauschen wir es bei Bedarf mit dem ersten unsortierten Element aus.
Wir wiederholen diesen Vorgang, bis das gesamte Array sortiert ist.

  
  
  LeetCode-Probleme lösen


Lösen wir ein Problem mit dem Leetcode-Algorithmus mithilfe des Auswahlsortierungsalgorithmus. Sollen wir?

  
  
  Problem: Ein Array sortieren [Mittel]


Problem: Sortieren Sie bei einem gegebenen Array von Ganzzahlen das Array in aufsteigender Reihenfolge und geben Sie es zurück. Sie müssen das Problem ohne Verwendung integrierter Funktionen in O(nlog(n)) Zeitkomplexität und mit der geringstmöglichen räumlichen Komplexität lösen.

Ansatz:: Um dieses Problem zu lösen, können wir den Selection Sort-Algorithmus direkt anwenden. Dies beinhaltet das Durchlaufen des Arrays, das Finden des kleinsten Elements im unsortierten Teil und den Austausch mit dem ersten unsortierten Element. Wir wiederholen diesen Vorgang, bis das gesamte Array sortiert ist.

Lösung:

// This function sorts an array of integers in ascending order using the Selection Sort algorithm.
const sortArray = function (nums) {
  // Get the length of the input array.
  const n = nums.length;

  // Iterate through the array, starting from the first element.
  for (let i = 0; i 


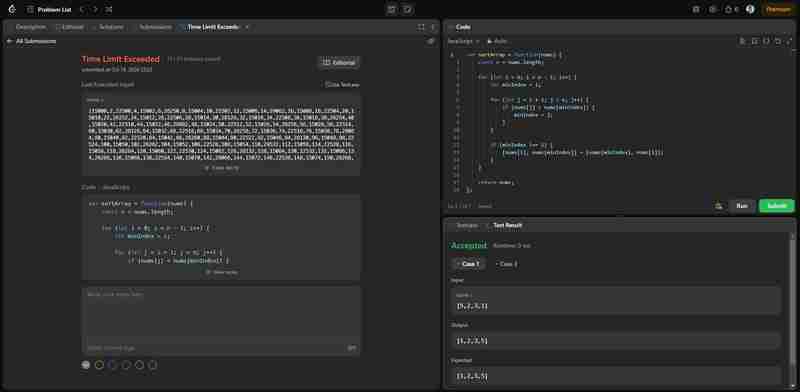
Diese Lösung wendet direkt den zuvor implementierten Auswahlsortierungsalgorithmus an. Obwohl das Problem dadurch korrekt gelöst wird, ist es erwähnenswert, dass diese Lösung aufgrund der O(n^2)-Zeitkomplexität der Auswahlsortierung möglicherweise das Zeitlimit für große Eingaben in LeetCode überschreitet. Das Bild unten zeigt, dass die Lösung korrekt, aber nicht effizient ist.



  
  
  Abschluss


Zusammenfassend lässt sich sagen, dass Selection Sort ein einfacher und intuitiver Sortieralgorithmus ist, der als hervorragender Einstieg in die Welt der Sortiertechniken dient. Aufgrund seiner Einfachheit ist es leicht zu verstehen und umzusetzen, was es zu einem wertvollen Lernwerkzeug für Anfänger macht. Aufgrund seiner quadratischen Zeitkomplexität O(n^2) ist es jedoch für große Datensätze nicht effizient. Für größere Datensätze oder leistungskritische Anwendungen werden effizientere Algorithmen wie QuickSort, MergeSort oder integrierte Sortierfunktionen bevorzugt.


  
  
  Bleiben Sie auf dem Laufenden und verbunden


Um sicherzustellen, dass Sie keinen Teil dieser Serie verpassen und um mit mir in Kontakt zu treten, um mehr darüber zu erfahren

Diskussionen über Softwareentwicklung (Web, Server, Mobil oder Scraping/Automatisierung), Daten

Strukturen und Algorithmen und andere spannende Technologiethemen, folgen Sie mir auf:



    
      

        
    
  

    

Die großartige Lösung?Folgen

    

      Softwareentwickler | Technischer Redakteur | Backend-, Web- und Mobilentwickler? | Leidenschaft für die Entwicklung effizienter und skalierbarer Softwarelösungen. #letsconnect ?
    
  

• GitHub
• Linkedin
• X (Twitter)

Bleiben Sie dran und viel Spaß beim Codieren ?‍??