Dieser Abschnitt enthält mehrere Beispiele für die Bestimmung von Big O für Wiederholungs-, Sequenz- und Auswahlanweisungen.

Beispiel 1

Berücksichtigen Sie die zeitliche Komplexität für die folgende Schleife:

for (int i = 1; i k = k 5;
}

Es ist eine konstante Zeit, c, für die Ausführung

k = k 5;

Da die Schleife n-mal ausgeführt wird, beträgt die zeitliche Komplexität für die Schleife

T(n) = (eine Konstante c)*n = O(n).

Die theoretische Analyse sagt die Leistung des Algorithmus voraus. Um zu sehen, wie dieser Algorithmus funktioniert, führen wir den Code im folgenden Programm aus, um die Ausführungszeit für n = 1000000, 10000000, 100000000 und 100000000 zu erhalten.

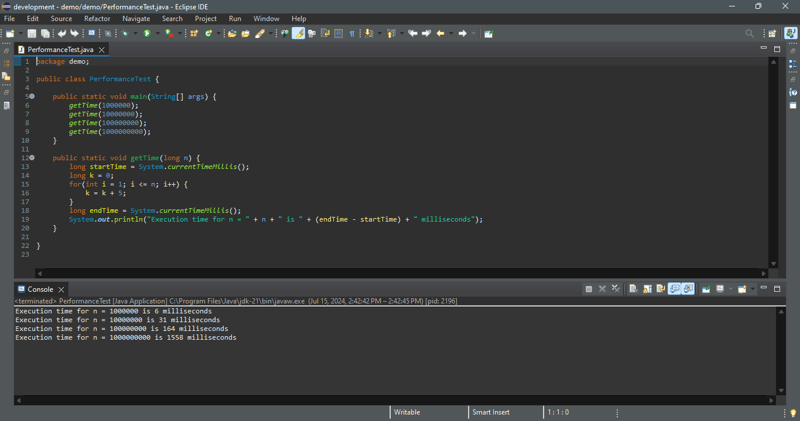
Unsere Analyse sagt eine lineare Zeitkomplexität für diese Schleife voraus. Wie in der Beispielausgabe gezeigt, erhöht sich die Laufzeit ungefähr um das Zehnfache, wenn die Eingabegröße um das Zehnfache erhöht wird. Die Ausführung bestätigt die Vorhersage.

Beispiel 2

Wie groß ist die zeitliche Komplexität für die folgende Schleife?

for (int i = 1; i for (int j = 1; j k = k i j;
}
}

Es ist eine konstante Zeit, c, für die Ausführung

k = k i j;

Die äußere Schleife wird n-mal ausgeführt. Für jede Iteration in der äußeren Schleife wird die innere Schleife n-mal ausgeführt. Somit beträgt die zeitliche Komplexität für die Schleife

T(n) = (eine Konstante c)*n*n = O(n^2)

Ein Algorithmus mit der Zeitkomplexität O(n^2) wird als quadratischer Algorithmus bezeichnet und weist eine quadratische Wachstumsrate auf. Der quadratische Algorithmus wächst schnell mit zunehmender Problemgröße. Wenn Sie die Eingabegröße verdoppeln, vervierfacht sich die Zeit für den Algorithmus. Algorithmen mit einer verschachtelten Schleife sind oft quadratisch.

Beispiel 3

Betrachten Sie die folgende Schleife:

for (int i = 1; i for (int j = 1; j k = k i j;
}
}

Die äußere Schleife wird n-mal ausgeführt. Für i = 1, 2, c wird die innere Schleife einmal, zweimal und n-mal ausgeführt. Somit beträgt die zeitliche Komplexität für die Schleife

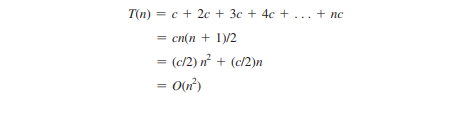
Beispiel 4

Betrachten Sie die folgende Schleife:

for (int i = 1; i for (int j = 1; j k = k i j;
}
}

Die innere Schleife wird 20-mal und die äußere Schleife n-mal ausgeführt. Daher beträgt die zeitliche Komplexität für die Schleife

T(n) = 20*c*n = O(n)

Beispiel 5

Betrachten Sie die folgenden Sequenzen:

for (int j = 1; j k = k 4;
}

for (int i = 1; i for (int j = 1; j k = k i j;
}
}

Die erste Schleife wird 10 Mal und die zweite Schleife 20 * n Mal ausgeführt. Somit beträgt die zeitliche Komplexität für die Schleife

T(n) = 10*c 20*c*n = O(n)

Beispiel 6

Betrachten Sie die folgende Auswahlanweisung:

if (list.contains(e)) {
System.out.println(e);
}
anders
for (Objekt t: Liste) {
System.out.println(t);
}

Angenommen, die Liste enthält n Elemente. Die Ausführungszeit für list.contains(e) beträgt O(n). Die Schleife in der Klausel else benötigt O(n) Zeit. Daher beträgt die Zeitkomplexität für die gesamte Anweisung

Beispiel 7

Betrachten Sie die Berechnung von a^n für eine ganze Zahl n. Ein einfacher Algorithmus würde a n-mal multiplizieren, wie folgt:

result = 1;
for (int i = 1; i Ergebnis *= a;

Der Algorithmus benötigt O(n) Zeit. Nehmen Sie ohne Beschränkung der Allgemeinheit an, dass n = 2^k ist. Sie können den Algorithmus mithilfe des folgenden Schemas verbessern:

result = a;
for (int i = 1; i Ergebnis = Ergebnis * Ergebnis;

Der Algorithmus benötigt O(logn) Zeit. Für ein beliebiges n können Sie den Algorithmus überarbeiten und beweisen, dass die Komplexität immer noch O(logn) ist.

Da 0(logn) = 0(log2n) = 0(logan) ist, wird der Einfachheit halber die konstante Basis weggelassen.