بيان المشكلة 1071. القاسم المشترك الأكبر للسلاسل

بالنسبة إلى سلسلتين s وt، نقول "t يقسم s" إذا وفقط إذا كانت s = t t t ... t t (أي، t متسلسلة مع نفسها مرة واحدة أو أكثر).

بالنظر إلى سلسلتين str1 وstr2، قم بإرجاع أكبر سلسلة x بحيث تقسم x كلا من str1 وstr2.

عملية تفكيري

على الرغم من أن رمز leetcode قد وضع علامة عليها على أنها مشكلة سهلة، إلا أنني يجب أن أعترف أنني وجدت صعوبة في التوصل إلى حل على الفور.

اسمح لي بمراجعة حالات الاختبار المقدمة من leetcode ومراجعتها لشرح حيرتي.

حالات الاختبار

الإدخال: str1 = "ABCABC"، str2 = "ABC"
الإخراج: "ABC"

الإدخال: str1 = "ABABAB"، str2 = "ABAB"
الإخراج: "AB"

من بيان المشكلة وحالة الاختبار 1، حددت أننا بحاجة إلى إخراج أكبر سلسلة ("ABC") متسلسل يمكننا الحصول على كلتا السلسلتين. (السلسلة الافتراضية "ABC" === str2 و"ABC" "ABC" === str1).

ومع ذلك، عند النظر إلى حالة الاختبار 2، أدركت بسرعة أن فهمي لم يكن صحيحًا لأنه وفقًا لذلك يجب أن أخرج "ABAB" لأن هذه هي أطول سلسلة يمكنني من خلالها إنشاء كلا السلسلتين. لكنني قفزت إلى البرمجة وبدأت في رسم حل. (خطأ مبتدئ؟)

ما فشل/نجح

لم أتمكن من رسم حل إلا عندما:

1. ابحث عن GCD لسلسلتين.
2. التكرار من طول أصغر سلسلة إلى GCD
3. خذ سلسلة فرعية من أصغر سلسلة إلى قيمة التكرار الحالية.
4. إذا كانت كلتا السلاسل تحتوي على تلك السلسلة الفرعية، قم بإرجاع تلك السلسلة الفرعية كإجابة.
5. إذا لم يتم العثور على سلسلة، قم بإرجاع "".

كما ترون فشل الحل الخاص بي للسلاسل حيث يحتوي str1 على str2 ولكنه يحتوي أيضًا على بعض الأحرف الإضافية الأخرى. مخالفة شرط أن s = t t ... t t.

اضطررت إلى اللجوء إلى حل neetcode للحصول على المساعدة. لقد فهمت مشاكلي بسرعة:

1. كنت أجد GCD لطول السلسلة، وليس السلسلة نفسها. أحتاج إلى العثور على سلسلة حيث يمكنني من خلال تكرار تلك السلاسل إنشاء كلا السلسلتين دون أي أحرف متبقية.

2. أدركت لماذا لا يمكن أن يكون "ABAB" هو الحل لحالة الاختبار 2:

• نحن بحاجة إلى العثور على x بحيث يقسم كلا السلاسل بالتساوي. لذا، باستخدام "ABABAB" كسلسلة، يمكنك إنشاء str2 بالكامل ولكن بالنسبة إلى str1 ينتهي بك الأمر بـ "ABABABAB". ينتهي بك الأمر مع 2 "AB" زائدين ولا يمكنك القول أنك قمت بإنشاء str1 بالكامل من خلال الجمع بين x.

• طول "ABAB" 4 وطول "ABABAB" 6. GCD للسلسلتين = 2. ومن ثم يجب أن يكون الإخراج سلسلة بطول 2.

الإخراج

تعقيد الزمان والمكان

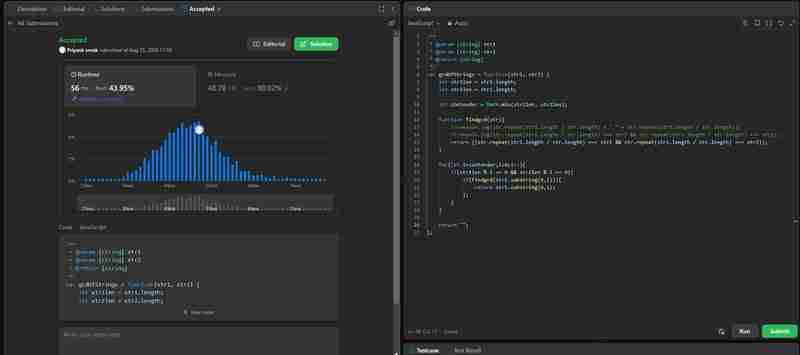
تعقيد الوقت: في أسوأ الحالات، نقوم بالتكرار على Min(str1,str2) ونحتاج إلى إعادة إنشاء str1 وstr2 بحيث يكون (str1.length str2.length) لذا فإن التعقيد الزمني الإجمالي سيكون O(min(str1,str2) * (str1.length str2.length))

تعقيد المساحة: O(1) حيث أننا لا نحتاج إلى أي مساحة إضافية.