يتم السخرية من جافا سكريبت بشكل متكرر عندما يواجه المطورون هذه النتيجة التي تبدو محيرة لأول مرة:

0.1   0.2 == 0.30000000000000004

تنتشر الميمات حول تعامل جافا سكريبت مع الأرقام على نطاق واسع، مما يدفع الكثيرين في كثير من الأحيان إلى الاعتقاد بأن هذا السلوك فريد بالنسبة للغة.

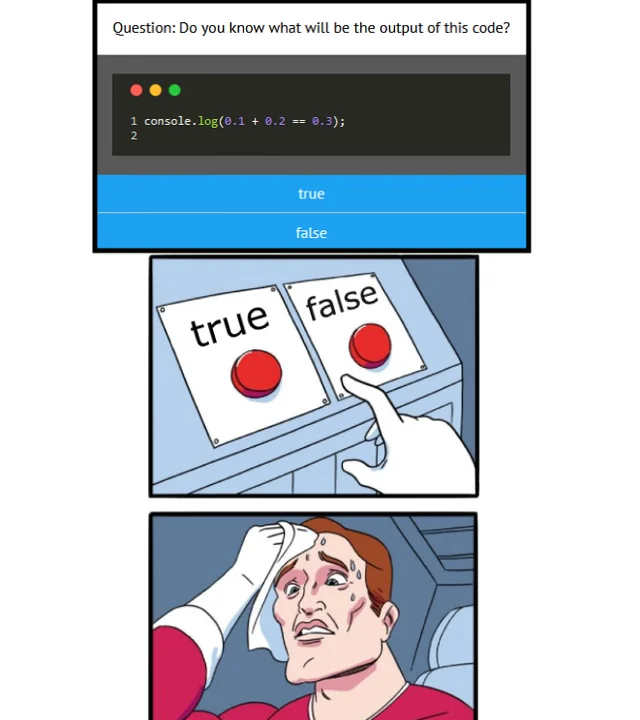
ومع ذلك، لا يقتصر هذا الأمر الغريب على جافا سكريبت فقط. إنه نتيجة لكيفية تعامل معظم لغات البرمجة مع حساب الفاصلة العائمة.

على سبيل المثال، فيما يلي مقتطفات التعليمات البرمجية من Java وGo التي تنتج نتائج مماثلة:

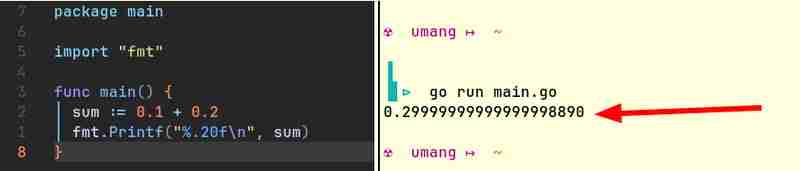
يمكن لأجهزة الكمبيوتر تخزين الأعداد الصحيحة فقط. إنهم لا يفهمون الكسور. (كيف سيفعلون ذلك؟ الطريقة الوحيدة التي تستطيع بها أجهزة الكمبيوتر إجراء العمليات الحسابية هي تشغيل بعض الأضواء أو إطفائها. يمكن أن يكون الضوء مضاءً أو مطفأً. ولا يمكن أن يكون مضاءً "نصفًا"!) إنهم بحاجة إلى طريقة ما لتمثيل أرقام الفاصلة العائمة. . وبما أن هذا التمثيل ليس دقيقًا تمامًا، ففي أغلب الأحيان، 0.1 0.2 لا يساوي 0.3.

يمكن التعبير بشكل واضح عن جميع الكسور التي تتكون مقاماتها من عوامل أولية لقاعدة نظام الأرقام، بينما تحتوي أي كسور أخرى على أعداد عشرية متكررة. على سبيل المثال، في نظام الأعداد ذو الأساس 10، يتم تمثيل الكسور مثل 1/2، 1/4، 1/5، 1/10 بشكل واضح لأن المقامات في كل حالة تتكون من 2 أو 5 - العوامل الأولية للرقم 10 ومع ذلك، فإن الكسور مثل 1/3، 1/6، 1/7 تحتوي جميعها على أعداد عشرية متكررة.

وبالمثل، في كسور النظام الثنائي مثل 1/2، 1/4، 1/8 يتم التعبير عنها بشكل واضح في حين أن جميع الكسور الأخرى لها أعداد عشرية متكررة. عندما تقوم بإجراء عملية حسابية على هذه الكسور العشرية المتكررة، ينتهي بك الأمر مع بقايا الطعام التي يتم ترحيلها عند تحويل التمثيل الثنائي للكمبيوتر للأرقام إلى تمثيل على أساس 10 يمكن قراءته بواسطة الإنسان. وهذا ما يؤدي إلى نتائج صحيحة تقريبًا.

الآن بعد أن تأكدنا من أن هذه المشكلة لا تقتصر على JavaScript، فلنستكشف كيفية تمثيل أرقام الفاصلة العائمة ومعالجتها لفهم سبب حدوث هذا السلوك.

من أجل فهم كيفية تمثيل ومعالجة أرقام الفاصلة العائمة تحت الغطاء، علينا أولاً أن نفهم معيار النقطة العائمة IEEE 754.

معيار IEEE 754 هو مواصفة مستخدمة على نطاق واسع لتمثيل وتنفيذ العمليات الحسابية على أرقام الفاصلة العائمة في أنظمة الكمبيوتر. تم إنشاؤه لضمان الاتساق عند استخدام حساب الفاصلة العائمة على منصات الحوسبة المختلفة. تلتزم معظم لغات البرمجة وتطبيقات الأجهزة (وحدات المعالجة المركزية، ووحدات معالجة الرسومات، وما إلى ذلك) بهذا المعيار.

هذه هي الطريقة التي تتم بها الإشارة إلى الرقم بتنسيق IEEE 754:

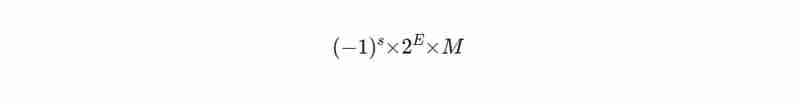
هنا s هي بت الإشارة (0 للموجب، 1 للسالب)، M هي الجزء العشري (يحتوي على أرقام الرقم) و E هو الأس الذي يحدد مقياس الرقم.

لن تتمكن من العثور على أي قيم صحيحة لـ M وE يمكن أن تمثل بالضبط أرقامًا مثل 0.1 أو 0.2 أو 0.3 بهذا التنسيق. يمكننا فقط اختيار قيم M وE التي تعطي النتيجة الأقرب.

إليك أداة يمكنك استخدامها لتحديد ترميزات IEEE 754 للأرقام العشرية: https://www.h-schmidt.net/FloatConverter/IEEE754.html

IEEE 754 تدوين 0.25:

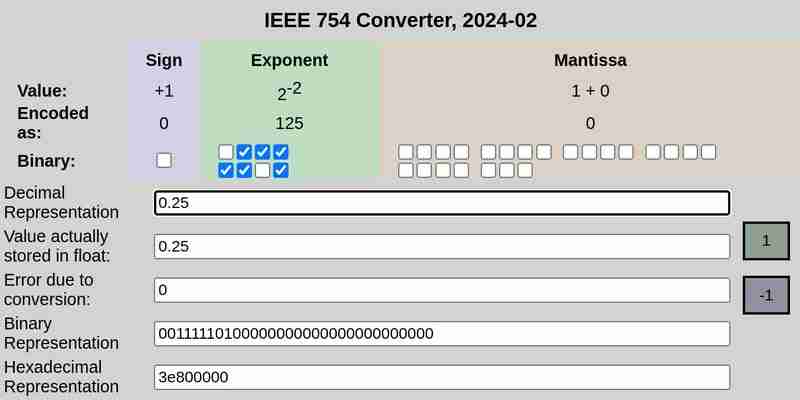
IEEE 754 تدوين 0.1 و 0.2 على التوالي:

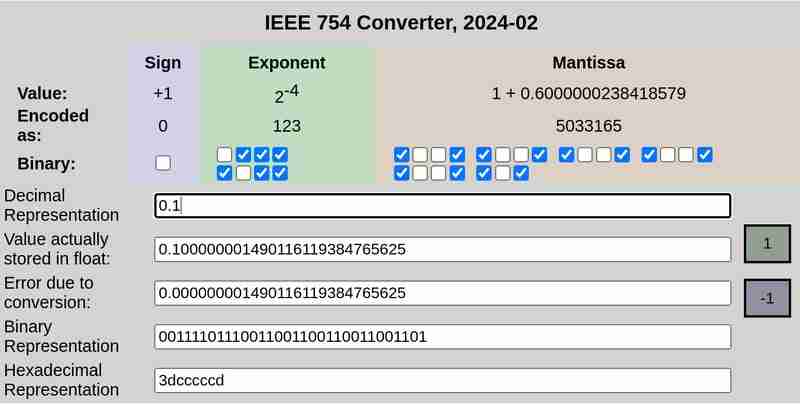
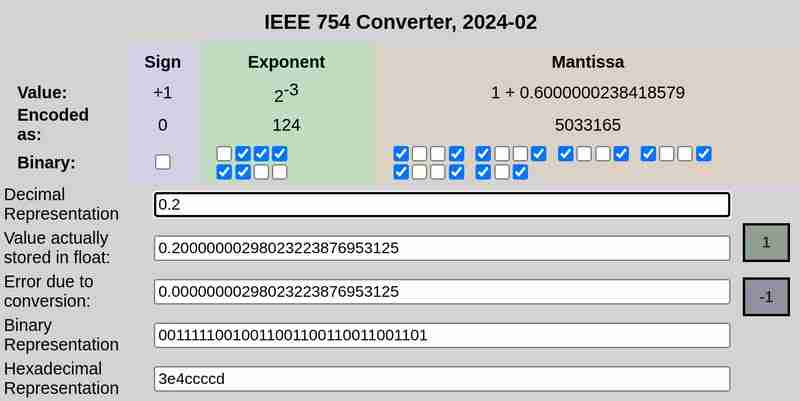
يرجى ملاحظة أن الخطأ الناتج عن التحويل في حالة 0.25 كان 0، بينما كان 0.1 و0.2 أخطاء غير صفرية.

IEEE 754 يحدد التنسيقات التالية لتمثيل أرقام الفاصلة العائمة:

• الدقة الفردية (32 بت): 1 بت للعلامة، 8 بت للأس، 23 بت للجزء العشري

• دقة مزدوجة (64 بت): 1 بت للعلامة، 11 بت للأس، 52 بت للجزء العشري

من أجل التبسيط، دعونا نفكر في التنسيق أحادي الدقة الذي يستخدم 32 بت.

التمثيل 32 بت لـ 0.1 هو:

0 01111011 10011001100110011001101

هنا تمثل البتة الأولى الإشارة (0 مما يعني موجب في هذه الحالة)، والبتات الثمانية التالية (01111011) تمثل الأس والبتات الـ 23 الأخيرة (10011001100110011001101) تمثل الجزء العشري.

هذا ليس تمثيلًا دقيقًا. يمثل ≈ 0.100000001490116119384765625

وبالمثل، تمثيل 32 بت لـ 0.2 هو:

0 01111100 10011001100110011001101

وهذا ليس تمثيلًا دقيقًا أيضًا. يمثل ≈ 0.20000000298023223876953125

عند الإضافة ينتج:

0 01111101 11001101010011001100110 

وهو ≈ 0.30000001192092896 بالتمثيل العشري.

في الختام، فإن النتيجة التي تبدو محيرة وهي 0.1 0.2 والتي لا تنتج 0.3 ليست شذوذًا خاصًا بجافا سكريبت، ولكنها نتيجة لقيود حساب الفاصلة العائمة عبر لغات البرمجة. تكمن جذور هذا السلوك في التمثيل الثنائي للأرقام، والذي يؤدي بطبيعته إلى أخطاء في الدقة عند التعامل مع كسور معينة.