يقدم هذا القسم خوارزميات فعالة للعثور على أقرب زوج من النقاط باستخدام طريقة فرق تسد. بالنظر إلى مجموعة من النقاط، فإن مسألة الزوج الأقرب هي إيجاد النقطتين الأقرب إلى بعضهما البعض. كما هو موضح في الشكل أدناه، يتم رسم خط لتوصيل أقرب نقطتين في الرسم المتحرك لأقرب زوج.

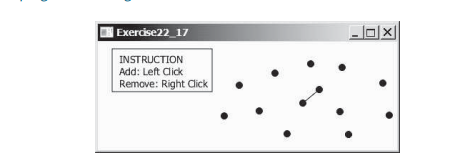
دراسة الحالة: العثور على أقرب زوج، قدمت خوارزمية القوة الغاشمة للعثور على أقرب زوج من النقاط. تحسب الخوارزمية المسافات بين جميع أزواج النقاط وتجد النقطة ذات الحد الأدنى للمسافة. من الواضح أن الخوارزمية تستغرق وقتًا O(n^2). هل يمكننا تصميم خوارزمية أكثر كفاءة؟

سوف نستخدم طريقة تسمى فرق تسد لحل هذه المشكلة. يقسم هذا المنهج المشكلة إلى مشكلات فرعية، ويحل المشكلات الفرعية، ثم يجمع حلول المشكلات الفرعية للحصول على حل للمشكلة بأكملها. على عكس نهج البرمجة الديناميكية، فإن المشاكل الفرعية في نهج فرق تسد لا تتداخل. المشكلة الفرعية تشبه المشكلة الأصلية بحجم أصغر، لذا يمكنك تطبيق التكرار لحل المشكلة. في الواقع، جميع الحلول للمشاكل العودية تتبع منهج فرق تسد.

توضح الخطوات أدناه كيفية حل مشكلة الزوج الأقرب باستخدام أسلوب فرق تسد.

• الخطوة 1: فرز النقاط بترتيب تصاعدي لإحداثيات x. بالنسبة للنقاط التي لها نفس إحداثيات x، قم بالفرز حسب إحداثيات y. ينتج عن هذا قائمة مرتبة S من النقاط.
• الخطوة 2: قسّم S إلى مجموعتين فرعيتين، S1 وS2، متساويتين في الحجم باستخدام نقطة المنتصف في القائمة التي تم فرزها. دع نقطة المنتصف تكون في S1. ابحث بشكل متكرر عن أقرب زوج في S1 وS2. دع d1 وd2 يشيران إلى مسافة أقرب الأزواج في المجموعتين الفرعيتين، على التوالي.
• الخطوة 3: ابحث عن أقرب زوج بين نقطة في S1 ونقطة في S2 وحدد المسافة بينهما بـ d3. أقرب زوج هو الذي تبعد عنه المسافة min(d1, d2, d3).

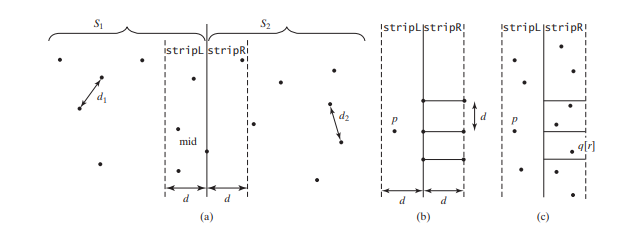
يستغرق فرز التحديد وقتًا O(n^2). يمكن تنفيذ الخطوة 1 في زمن O(n log n). يمكن تنفيذ الخطوة 3 في وقت O(n). دع د = دقيقة (د1، د2). نحن نعلم بالفعل أن أقرب مسافة زوجية لا يمكن أن تكون أكبر من d. بالنسبة لنقطة في S1 ونقطة في S2 لتشكيل أقرب زوج في S، يجب أن تكون النقطة اليسرى في stripL والنقطة اليمنى في stripR، كما هو موضح في الشكل أدناه ( أ).

بالنسبة لنقطة p في stripL، ما عليك سوى النظر في نقطة قائمة داخل المستطيل d X 2d، كما هو موضح أدناه (ب). لا يمكن لأي نقطة قائمة خارج المستطيل أن تشكل أقرب زوج مع p. نظرًا لأن مسافة أقرب زوج في S2 أكبر من أو تساوي d، فيمكن أن يكون هناك ستة
على الأكثر نقاط في المستطيل. وبالتالي، لكل نقطة في stripL، يجب أخذ ست نقاط على الأكثر في stripR في الاعتبار.

لكل نقطة p في stripL، كيف يمكنك تحديد موقع النقاط في منطقة المستطيل d X 2d المقابلة في stripR؟ يمكن القيام بذلك بكفاءة إذا تم فرز النقاط في stripL و stripR بترتيب متزايد لإحداثيات y الخاصة بها. اجعل pointsOrderedOnY هي قائمة النقاط مرتبة بترتيب متزايد لإحداثيات y. يمكن الحصول على pointsOrderedOnY مسبقًا في الخوارزمية. يمكن الحصول على stripL وstripR من pointsOrderedOnY في الخطوة 3 كما هو موضح في الكود أدناه.

لكل نقطة p بالنقاطOrderedOnY
إذا (p موجود في S1 وmid.x - p.x إلحاق p بـ stripL;
آخر إذا (p موجود في S2 وp.x - mid.x إلحاق p بـ stripR؛

اجعل النقاط في stripL و stripR هي {p0, p1, ... , pk} و{q0, q1,... , qt}، كما هو موضح في الشكل أعلاه (ج). يمكن العثور على أقرب زوج بين نقطة في stripL ونقطة في stripR باستخدام الخوارزمية الموضحة في الكود أدناه.

d = min(d1, d2);
 r = 0; // r is the index of a point in stripR
 for (each point p in stripL) {
 // Skip the points in stripR below p.y - d
  while (r 



النقاط الموجودة في stripL تعتبر من p0، p1، ... ، pk بهذا الترتيب. للحصول على نقطة p في stripL، تخطي النقاط في stripR الموجودة أسفل p.y – d (السطور 5-6). بمجرد تخطي نقطة، لن يتم أخذها في الاعتبار. تتحقق حلقة while (السطور 9-17) مما إذا كان (p, q[r1]) هو أقرب زوج محتمل. يوجد ستة أزواج من q[r1] على الأكثر، لأن المسافة بين نقطتين في stripR لا يمكن أن تكون أقل من d. وبالتالي فإن تعقيد العثور على أقرب زوج في الخطوة 3 هو O(n).

لاحظ أن الخطوة 1 في الخطوات أعلاه يتم تنفيذها مرة واحدة فقط لفرز النقاط مسبقًا. افترض أن جميع النقاط تم فرزها مسبقًا. دع T(n) يشير إلى التعقيد الزمني لهذه الخوارزمية. هكذا،



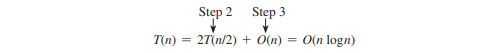
لذلك، يمكن العثور على أقرب زوج من النقاط في زمن O(n log n).