تصميم الخوارزميات هو تطوير عملية رياضية لحل مشكلة ما. تحليل الخوارزمية هو التنبؤ بأداء الخوارزمية. قدم الفصلان السابقان هياكل البيانات الكلاسيكية (القوائم، والمكدسات، وطوابير الانتظار، وقوائم الانتظار ذات الأولوية، والمجموعات، والخرائط) وطبقوها لحل المشكلات. سيستخدم هذا الفصل مجموعة متنوعة من الأمثلة لتقديم تقنيات خوارزمية شائعة (البرمجة الديناميكية، فرق تسد، والتتبع الخلفي) لتطوير خوارزميات فعالة.

يحصل تدوين Big O على وظيفة لقياس تعقيد وقت الخوارزمية بناءً على حجم الإدخال. يمكنك تجاهل الثوابت المضاعفة والمصطلحات غير المسيطرة في الدالة. لنفترض أن خوارزميتين تؤديان نفس المهمة، مثل البحث (البحث الخطي مقابل البحث الثنائي). أيهما أفضل؟ للإجابة على هذا السؤال، يمكنك تنفيذ هذه الخوارزميات وتشغيل البرامج للحصول على وقت التنفيذ. ولكن هناك مشكلتان في هذا النهج:

أولاً، يتم تشغيل العديد من المهام بشكل متزامن على جهاز الكمبيوتر. يعتمد وقت تنفيذ برنامج معين على تحميل النظام.
ثانيًا، يعتمد وقت التنفيذ على مدخلات محددة. خذ بعين الاعتبار، على سبيل المثال، البحث الخطي والبحث الثنائي. إذا كان العنصر المطلوب البحث عنه هو الأول في القائمة، فإن البحث الخطي سيجد العنصر بشكل أسرع من البحث الثنائي.

من الصعب جدًا مقارنة الخوارزميات عن طريق قياس وقت تنفيذها. للتغلب على هذه المشاكل، تم تطوير نهج نظري لتحليل الخوارزميات المستقلة عن أجهزة الكمبيوتر ومدخلات محددة. يقترب هذا الأسلوب من تأثير التغيير على حجم الإدخال. بهذه الطريقة، يمكنك معرفة مدى سرعة زيادة وقت تنفيذ الخوارزمية مع زيادة حجم الإدخال، بحيث يمكنك مقارنة خوارزميتين من خلال فحص

معدلات النمو.

فكر في البحث الخطي. تقوم خوارزمية البحث الخطي بمقارنة المفتاح بالعناصر الموجودة في المصفوفة بشكل تسلسلي حتى يتم العثور على المفتاح أو استنفاد المصفوفة. إذا لم يكن المفتاح موجودًا في المصفوفة، فإنه يتطلب مقارنات

n لمصفوفة ذات حجم n. إذا كان المفتاح موجودًا في المصفوفة، فإنه يتطلب مقارنات n/2 في المتوسط. يتناسب وقت تنفيذ الخوارزمية مع حجم المصفوفة. إذا قمت بمضاعفة حجم المصفوفة، فسوف تتوقع أن يتضاعف عدد المقارنات. تنمو الخوارزمية بمعدل خطي. معدل النمو له حجم n. يستخدم علماء الكمبيوتر رمز Big O لتمثيل "ترتيب الحجم". باستخدام هذا الترميز، يكون تعقيد خوارزمية البحث الخطي هو O(n)، ويتم نطقه كـ "order of n." نحن نسمي الخوارزمية ذات التعقيد الزمني O(n) خوارزمية خطية، وتظهر معدل نمو خطي.

بالنسبة لنفس حجم الإدخال، قد يختلف وقت تنفيذ الخوارزمية، اعتمادًا على الإدخال. يُطلق على الإدخال الذي يؤدي إلى أقصر وقت تنفيذ اسم

إدخال أفضل حالة، والمدخل الذي يؤدي إلى أطول وقت تنفيذ هو إدخال أسوأ حالة. تحليل أفضل الحالات و تحليل أسوأ الحالات هو تحليل الخوارزميات لمعرفة مدخلات أفضل الحالات ومدخلات أسوأ الحالات. إن تحليل أفضل الحالات وأسوأها ليسا تمثيليين، ولكن تحليل أسوأ الحالات مفيد للغاية. يمكنك التأكد من أن الخوارزمية لن تكون أبدًا أبطأ من أسوأ الحالات.
يحاول
تحليل الحالة المتوسطة تحديد متوسط ​​مقدار الوقت بين جميع المدخلات الممكنة بنفس الحجم. يعد تحليل الحالة المتوسطة مثاليًا، ولكن من الصعب تنفيذه، لأنه من الصعب بالنسبة للعديد من المشكلات تحديد الاحتمالات والتوزيعات النسبية لمثيلات الإدخال المختلفة. يعتبر تحليل أسوأ الحالات أسهل في التنفيذ، لذلك يتم إجراء التحليل بشكل عام لأسوأ الحالات.

تتطلب خوارزمية البحث الخطي مقارنات

n في أسوأ الحالات ومقارنات n/2 في الحالة المتوسطة إذا كنت تبحث دائمًا تقريبًا عن شيء معروف بوجوده في القائمة. باستخدام تدوين Big O، تتطلب كلتا الحالتين وقت O(n). يمكن حذف الثابت المضاعف (1/2). ويركز تحليل الخوارزمية على معدل النمو. الثوابت المضاعفة ليس لها أي تأثير على معدلات النمو. معدل النمو لـ n/2 أو 100_n_ هو نفس معدل النمو لـ n، كما هو موضح في الجدول أدناه، معدلات النمو. ولذلك، O(n) = O(n/2) = O(100n).

ضع في اعتبارك الخوارزمية للعثور على الحد الأقصى لعدد العناصر في مجموعة من العناصر n. للعثور على الحد الأقصى للعدد إذا كان n هو 2، فإنه يتطلب مقارنة واحدة؛ إذا كان n هو 3، مقارنتين. بشكل عام، يستغرق الأمر مقارنات n - 1 للعثور على الحد الأقصى لعدد العناصر في قائمة n. تحليل الخوارزمية مخصص لحجم المدخلات الكبير. إذا كان حجم الإدخال صغيرًا، فليس هناك أهمية في تقدير كفاءة الخوارزمية. كلما زاد حجم n، فإن الجزء n في التعبير n - 1 يهيمن على التعقيد. يسمح لك تدوين Big O بتجاهل الجزء غير المسيطر (على سبيل المثال، -1 في

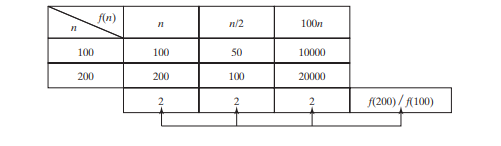
التعبير n - 1) وتسليط الضوء على الجزء المهم (على سبيل المثال، n في التعبير n - 1). ولذلك فإن تعقيد هذه الخوارزمية هو O(n).

يقدر تدوين Big O وقت تنفيذ الخوارزمية فيما يتعلق بحجم الإدخال. إذا لم يكن الوقت مرتبطًا بحجم الإدخال، يقال إن الخوارزمية تأخذ

وقتًا ثابتًا مع الإشارة O(1). على سبيل المثال، طريقة تقوم باسترداد عنصر في فهرس معين في صفيف يستغرق وقتًا ثابتًا، لأن الوقت لا ينمو مع زيادة حجم المصفوفة.

الملخصات الرياضية التالية غالبًا ما تكون مفيدة في تحليل الخوارزميات:

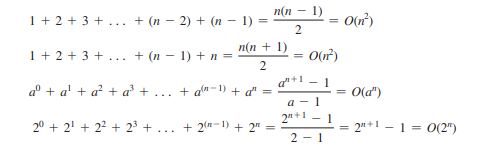
تعقيد الوقت هو مقياس لوقت التنفيذ باستخدام تدوين Big-O. وبالمثل، يمكنك أيضًا قياس تعقيد الفضاء باستخدام علامة Big-O. تعقيد المساحة يقيس مقدار مساحة الذاكرة التي تستخدمها الخوارزمية. التعقيد المكاني لمعظم الخوارزميات المعروضة في الكتاب هو O(n). أي أنها تظهر معدل نمو خطي لحجم المدخلات. على سبيل المثال، التعقيد المكاني للبحث الخطي هو O(n).