简介1

函数调用自身的过程称为递归，
相应的函数称为递归函数.
由于计算机编程是数学的基本应用，因此让
我们首先尝试理解递归背后的数学推理。
一般来说，我们都知道函数的概念。简而言之，函数是
提供输入时产生输出的数学方程。例如：
假设函数 F(x) 是由下式定义的函数： F(x) = x^2 4
我们可以将此函数的 Java 代码编写为：

公共静态 int F(int x){
返回 (x * x 4);
}

现在，我们可以将 x 的不同值传递给该函数并接收我们的输出
因此。
在继续递归之前，让我们尝试理解另一个数学
称为 数学归纳原理 (PMI) 的概念。

数学归纳原理 (PMI) 是一种证明陈述的技术，a
公式，或关于一组自然数的定理。它有
以下三步：
1.** 简单案例的步骤*：在这一步中，我们将证明
所需的陈述 基本情况，例如 n = 0 或 n = 1。
2.* 假设步骤**：在这一步中，我们将假设所需的语句
对于 n = k 有效。

1. 证明步骤：根据假设步骤的结果，我们将证明， 只要 n = k 为真，n = k 1 对于所需方程也成立。

例如：让我们用数学归纳法证明：
S(N): 1 2 3 ... N = (N * (N 1))/2
(前N个自然数之和)
证明：
步骤 1：当 N = 1 时，S(1) = 1 成立。
步骤 2：假设，对于 N = k，给定的陈述成立，即
1 2 3 .... k = (k * (k 1))/2
步骤 3：让我们使用步骤 2 来证明 N = k 1 的陈述。

证明： 1 2 3 ... (k 1) = ((k 1)*(k 2))/2
证明：

将(k 1)添加到步骤2获得的结果中的LHS和RHS：
1 2 3 ... (k 1) = (k*(k 1))/2 (k 1)

现在，从 RHS 端取 (k 1) common：
1 2 3 ... (k 1) = (k 1)*((k 2)/2)

根据我们试图证明的说法：
1 2 3 ... (k 1) = ((k 1)*(k 2))/2
由此证明。

递归的工作

总结以上三点我们就可以定义递归方法的步骤了
步骤：
● 基本情况：递归函数必须有一个终止条件，其中
该进程将停止调用自身。这种情况称为基本情况。如果没有基本情况，它将不断调用自身并陷入
无限循环。很快，就会超出递归深度*，并且会抛出
错误。
● 递归调用：递归函数将在较小的版本上调用自身
的主要问题。我们在编写此步骤时需要小心
正确找出你的小问题是什么至关重要。
● 小计算：一般我们在每个递归
中执行一次计算步骤 称呼。我们可以在递归调用之前或之后实现这个计算步骤
取决于问题的性质。

注意：递归使用存储递归调用的内置堆栈。因此，
递归调用的次数必须尽可能少，以避免内存溢出。如果
递归调用次数超过最大允许数量，
**将超过递归深度**。
现在，让我们看看如何使用递归解决一些常见问题

问题陈述 - 求一个数的阶乘

方法：找出 PMI 的三个步骤，然后使用
将其关联起来 递归

1. 归纳步骤：计算数字 n - F(n) 的阶乘 归纳假设：我们已经得到了n-1 - F(n-1)
的阶乘
2. 用F(n-1)表示F(n)：F(n)=n*F(n-1)。因此我们得到

public static int fact(int n){
int ans = 事实(n-1); #假设步骤
返回 ans * n； #从假设步骤解决问题
}

1. 代码仍然不完整。缺少的部分是基本情况。现在我们将 试运行以查找需要停止递归的情况。考虑 n = 5:

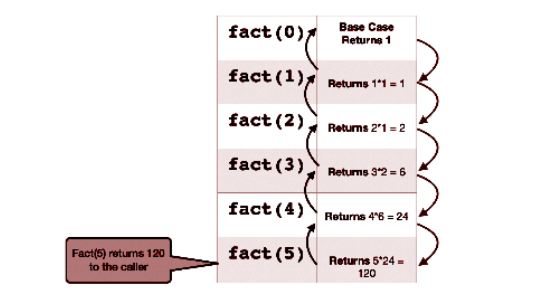
正如我们上面所看到的，我们已经知道n = 0的答案，即1。所以我们将
将此作为我们的基本情况。因此，代码现在变成：

公共静态 int 阶乘(int n){
if (n == 0) // 基本情况
返回 1;
别的
返回 n*阶乘(n-1); // 递归情况
}