正如我们一直在讨论不同的排序算法一样，今天我们将学习选择排序算法。一种排序算法，允许在内存受限的环境中实现尽可能少的交换。

目录

1. 介绍
2. 什么是选择排序算法？
3. 选择排序如何工作？
   • 时间复杂度
   • 空间复杂度
4. JavaScript 中的实现
5. 解决 LeetCode 问题
6. 结论

介绍

选择排序是一种简单而有效的排序算法，其工作原理是从列表的未排序部分中重复选择最小（或最大）元素，并将其移动到已排序部分的开头（或结尾）。重复这个过程，直到整个列表排序完成。在本文中，我们将深入研究选择排序算法的细节、它在 JavaScript 中的实现以及它在解决实际问题中的应用。

什么是选择排序算法？

选择排序算法是一种就地比较排序算法。它将输入列表分为两部分：

1. 左端排序后的部分
2. 右端未排序部分

该算法重复从未排序部分中选择最小元素，并将其与最左边的未排序元素交换，将已排序部分和未排序部分之间的边界向右移动一个元素。

选择排序如何工作？

让我们看一下使用数组 [64, 25, 12, 22, 11]:

1. 初始数组：[64,25,12,22,11]

• 排序部分：[]
• 未排序部分：[64,25,12,22,11]

1. 第一遍：

• 在未排序部分中查找最小值：11
• 将 11 与第一个未排序元素交换 (64)
• 结果：[11, 25, 12, 22, 64]
• 排序部分：[11]
• 未排序部分：[25, 12, 22, 64]

1. 第二遍：

• 在未排序部分中查找最小值：12
• 将 12 与第一个未排序元素 (25) 交换
• 结果：[11, 12, 25, 22, 64]
• 排序部分：[11, 12]
• 未排序部分：[25, 22, 64]

1. 第三遍：

• 在未排序部分中查找最小值：22
• 将 22 与第一个未排序元素 (25) 交换
• 结果：[11, 12, 22, 25, 64]
• 已排序部分：[11, 12, 22]
• 未排序部分：[25, 64]

1. 第四遍：

• 在未排序部分中查找最小值：25
• 25已经在正确的位置
• 结果：[11, 12, 22, 25, 64]
• 排序部分：[11, 12, 22, 25]
• 未排序部分：[64]

1. 最终通过：
   • 只剩下一个元素，它会自动位于正确的位置
   • 最终结果：[11,12,22,25,64]

数组现已完全排序。

时间复杂度

选择排序在所有情况下（最佳、平均和最差）的时间复杂度均为 O(n^2)，其中 n 是数组中元素的数量。这是因为：

• 外循环运行n-1次
• 对于外循环的每次迭代，内循环运行 n-i-1 次（其中 i 是外循环的当前迭代）

这会导致大约 (n^2)/2 次比较和 n 次交换，从而简化为 O(n^2)。

由于这种二次时间复杂度，选择排序对于大型数据集效率不高。然而，它的简单性以及它使交换次数尽可能少的事实使其在某些情况下很有用，特别是当辅助内存有限时。

空间复杂度

选择排序的空间复杂度为 O(1)，因为它对数组进行就地排序。无论输入大小如何，它只需要恒定数量的额外内存空间。这使得它具有内存效率，这在内存受限的环境中是有利的。

JavaScript 中的实现

这是选择排序算法的 JavaScript 实现：

function selectionSort(arr) {
  const n = arr.length;

  for (let i = 0; i 


我们来分解一下代码：

我们定义一个函数选择排序，它接受一个数组作为输入。
我们使用外循环 (i) 迭代数组，它表示已排序部分和未排序部分之间的边界。
对于每次迭代，我们假设第一个未排序元素是最小值并存储其索引。
然后我们使用内部循环 (j) 来查找未排序部分中实际的最小元素。
如果我们找到更小的元素，我们更新 minIndex。
找到最小值后，如有必要，我们将其与第一个未排序元素交换。
我们重复这个过程，直到整个数组排序完毕。

  
  
  解决 LeetCode 问题


让我们使用选择排序算法来解决一道 Leetcode 算法问题。我们可以？

  
  
  问题：对数组进行排序 [中]


问题：给定一个整数数组nums，按升序对数组进行排序并返回它。您必须在不使用任何内置函数的情况下以 O(nlog(n)) 时间复杂度和尽可能最小的空间复杂度解决问题。

做法：：解决这个问题，我们可以直接应用选择排序算法。这涉及迭代数组，找到未排序部分中的最小元素，并将其与第一个未排序元素交换。我们重复这个过程，直到整个数组排序完成。

解决方案：

// This function sorts an array of integers in ascending order using the Selection Sort algorithm.
const sortArray = function (nums) {
  // Get the length of the input array.
  const n = nums.length;

  // Iterate through the array, starting from the first element.
  for (let i = 0; i 


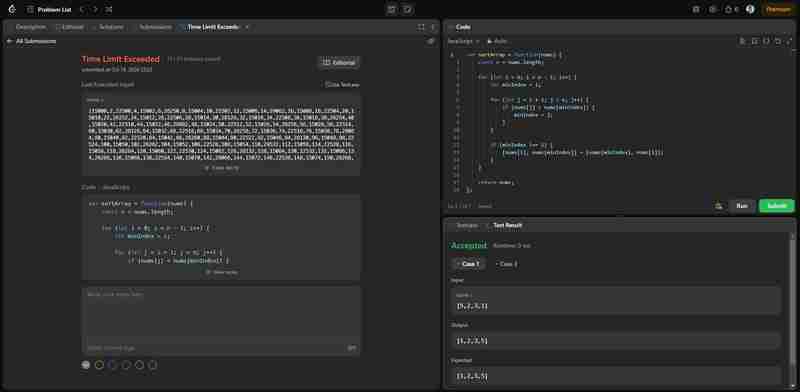
这个解决方案直接应用了我们之前实现的选择排序算法。虽然它正确地解决了问题，但值得注意的是，由于选择排序的 O(n^2) 时间复杂度，该解决方案可能会超出 LeetCode 上大量输入的时间限制。下图显示该解决方案是正确的，但效率不高。



  
  
  结论


总之，选择排序是一种简单直观的排序算法，可以很好地介绍排序技术的世界。它的简单性使其易于理解和实施，使其成为初学者有价值的学习工具。然而，由于其二次时间复杂度 O(n^2)，它对于大型数据集效率不高。对于较大的数据集或性能关键型应用程序，首选更高效的算法，例如 QuickSort、MergeSort 或内置排序函数。


  
  
  保持更新和联系


确保您不会错过本系列的任何部分，并与我联系以获得更深入的了解

关于软件开发（Web、服务器、移动或抓取/自动化）、数据的讨论

结构和算法，以及其他令人兴奋的技术主题，请关注我：



    
      

        
    
  

    

伟大的解决方案？关注

    

      软件工程师|技术撰稿人 |后端、网络和移动开发人员？ |热衷于打造高效且可扩展的软件解决方案。 #让连接？
    
  

• GitHub
• 领英
• X（推特）

敬请期待并快乐编码??‍??