加權九尾問題可以簡化為加權最短路徑問題。
部分提出了九尾問題並使用 BFS 演算法解決了它。本節介紹問題的變體並使用最短路徑演算法解決它。

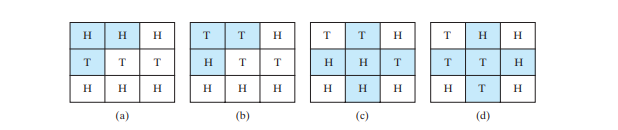
九尾問題是找出導致所有硬幣面朝下的最少移動次數。每一步都會翻轉一枚正面硬幣及其相鄰硬幣。加權九尾問題將翻轉次數指定為每次移動的權重。例如，您可以透過翻轉第一行中的第一個硬幣及其相鄰的兩個硬幣，將下圖a中的硬幣變更為下圖b中的硬幣。因此，此移動的權重為 3。透過翻轉中心硬幣及其四個相鄰硬幣，可以將下圖 c 中的硬幣變為下圖 d。所以這個動作的權重是5.

加權九尾問題可以簡化為在邊加權圖中尋找從起始節點到目標節點的最短路徑。該圖有 512 個節點。如果存在從節點 u 到節點 v 的移動，則建立從節點 v 到 u 的邊。將翻轉次數指定為邊的權重。

回想一下，在第 1 節中，我們定義了一個類別 NineTailModel 來建模九尾問題。我們現在定義一個名為WeightedNineTailModel的新類，它擴展了NineTailModel，如下圖所示。

NineTailModel類別建立一個Graph並取得以目標節點511為根的Tree。 WeightedNineTailModel 與NineTailModel 相同，只不過它創建了一個WeightedGraph 並獲取了一個以目標節點為根的ShortestPathTree 511。 WeightedNineTailModel 擴展了 NineTailModel。方法 getEdges() 找出圖中的所有邊。 getNumberOfFlips(int u, int v) 方法傳回從節點 u 到節點 v 的翻轉次數。 getNumberOfFlips(int u) 方法傳回從節點 u 到目標節點的翻轉次數。

下面的程式碼實現了WeightedNineTailModel.

package demo;
import java.util.*;

public class WeightedNineTailModel extends NineTailModel {
    /** Construct a model */
    public WeightedNineTailModel() {
        // Create edges
        List edges = getEdges();

        // Create a graph
        WeightedGraph graph = new WeightedGraph(edges, NUMBER_OF_NODES);

        // Obtain a shortest path tree rooted at the target node
        tree = graph.getShortestPath(511);
    }

    /** Create all edges for the graph */
    private List getEdges() {
        // Store edges
        List edges = new ArrayList();

        for(int u = 0; u .ShortestPathTree)tree).getCost(u);
    }
}

WeightedNineTailModel 擴充 NineTailModel 來建構 WeightedGraph 來建模加權九尾問題（第 10-11 行）。對於每個節點u，getEdges() 方法尋找翻轉節點v 並將翻轉次數指定為邊的權重(v, u)（第30 行）。 getNumberOfFlips(int u, int v) 方法傳回從節點 u 到節點 v 的翻轉次數（第 38-47 行）。翻轉次數是
之間不同單元格的數量 兩個節點（第 44 行）。

WeightedNineTailModel 取得以目標節點 511 為根的 ShortestPathTree（第 14 行）。請注意，tree 是 NineTailModel 中定義的受保護資料字段，ShortestPathTree 是 Tree 的子類別。 NineTailModel 中定義的方法使用 tree 屬性。

getNumberOfFlips(int u)方法（第49-52行）傳回從節點u到目標節點的翻轉次數，即從節點開始的路徑成本u到目標節點。此成本可以透過呼叫 ShortestPathTree 類別中定義的 getCost(u) 方法來取得（第 51 行）。

下面的程式碼給了一個程序，提示使用者輸入一個初始節點，並顯示到達目標節點的最少翻轉次數。

打包示範； 導入java.util.Scanner； 公共類WeightedNineTail { 公共靜態無效主（字串[] args）{ // 提示使用者輸入九個幣的Hs和Ts System.out.print("請輸入最初的九個硬幣Hs和Ts："); 掃描器輸入 = new Scanner(System.in); String s = input.nextLine(); char[] 初始節點 = s.toCharArray(); WeightedNineTailModel 模型 = new WeightedNineTailModel(); java.util.List path = model.getShortestPath(NineTailModel.getIndex(initialNode)); System.out.println("拋硬幣的步驟是"); for (int i = 0; i package demo; import java.util.Scanner; public class WeightedNineTail { public static void main(String[] args) { // Prompt the user to enter nine coins' Hs and Ts System.out.print("Enter the initial nine coins Hs and Ts: "); Scanner input = new Scanner(System.in); String s = input.nextLine(); char[] initialNode = s.toCharArray(); WeightedNineTailModel model = new WeightedNineTailModel(); java.util.List path = model.getShortestPath(NineTailModel.getIndex(initialNode)); System.out.println("The steps to flip the coins are "); for (int i = 0; i 輸入最初的九個硬幣 Hs 和 Ts：HHHTTTHHH

拋硬幣的步驟是

哈哈哈

TT
呵呵

哈哈哈

THT
TT

TTT

TT
TT

翻轉次數為8

程式在第8行提示使用者輸入由

H和T組成的9個字母組成的初始節點作為字串，從字串（第9 行），創建模型（第11 行），取得從初始節點到目標節點的最短路徑（第12-13 行），顯示路徑中的節點（第16-17 行），並呼叫 getNumberOfFlips 取得到達目標節點所需的翻轉次數（第 20 行）。