簡單理解貝塞爾曲線。
想象一下,如果只能用直线、椭圆、圆,设计一辆线条流畅、外观复杂的汽车不是很困难吗?
1962年,法国工程师Pierre Bézier发表了贝塞尔曲线,最初用于汽车主体设计。
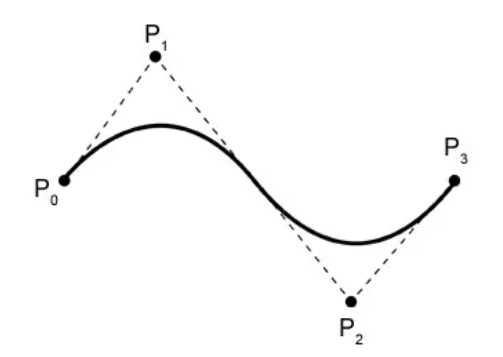
贝塞尔曲线可以通过一系列控制点定义一条平滑的曲线。曲线始终经过第一个和最后一个控制点,并受中间控制点形状的影响。此外,贝塞尔曲线具有凸包的属性。
贝塞尔曲线广泛应用于计算机图形和图像建模,例如动画、字体设计和工业设计。
公式
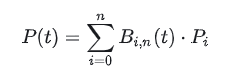
让我们了解一下。
P(t) 表示曲线上 t 处的点(t 是分数,取值范围为 0 到 1)。 t 处曲线上的点是什么?常见的曲线描述是:y = f(x),现在让我们将 P(t) 理解为 f(x)。不同的是,P(t)是参数表示(并且计算结果是[x,y]这样的“向量”),后面会详细解释
接下来,Pi表示第i个控制点(i从0开始)。以上图为例,有4个控制点,分别是P0、P1、P2、P3。公式中的n为控制点的最后一个索引,即n = 3(注意不是控制点的个数,而是计数减1)。
Bi,n(t) 是 Bernstein 基函数,也称为基函数。对于每个特定的(i,n),都有一个不同的基函数与之对应。如果从加权的角度理解,可以将基函数视为权重函数,表示第i个控制点Pi对t位置处的曲线坐标的“贡献”。
基函数的公式如下:
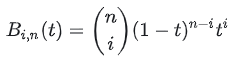
( in) 是组合数(从n中选择i有多少种方法?)。至于为什么基函数是这样的,可以结合De Casteljau算法来理解(见文中后面)
回到P(t)公式, Σi=0n 为求和符号,表示后续部分( i,n(t )⋅Pi ) 将从 i=0 到 i=n 求和。 以上图为例,假设我们要计算P(0.1),该怎么做呢?展开如下:
代入t=0.1得到:
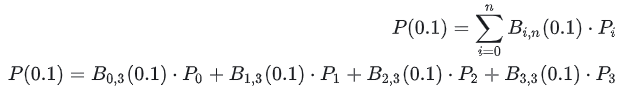
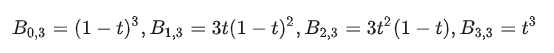 曲线的参数表示
曲线的参数表示
这里直接引用了网友的一篇文章(链接)
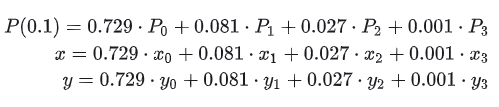
让我们重点关注上面的公式。
如上图所示,我们熟悉的直线可以从另一个角度来理解:用t(即|AP|从点P到已知点(x0,y0)的长度),那么通过上述三角函数就可以确定P点。
更一般的,可以写成: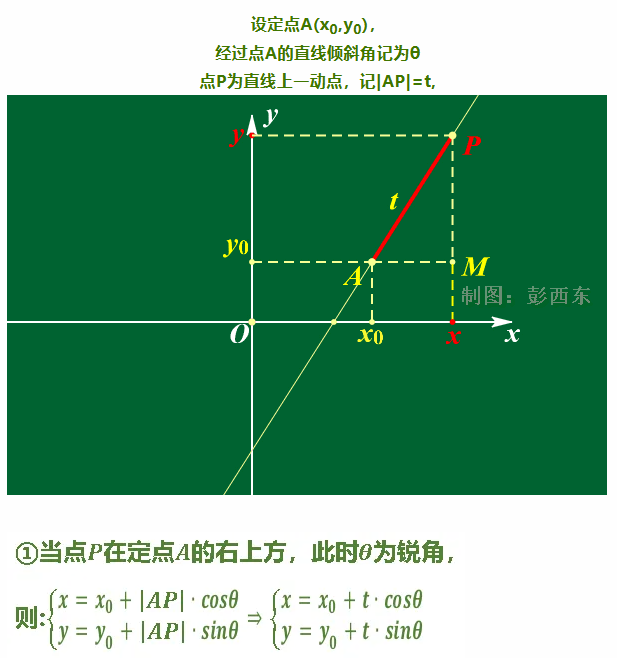
这里,P0是向量[x0,y0],v也是向量。加在一起时,P(t) 是向量 [x,y].
再看一下圆圈:
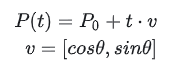
如图所示,圆可以看作有已知的圆心,圆上的任意点由旋转角度和半径确定。也可以写成:
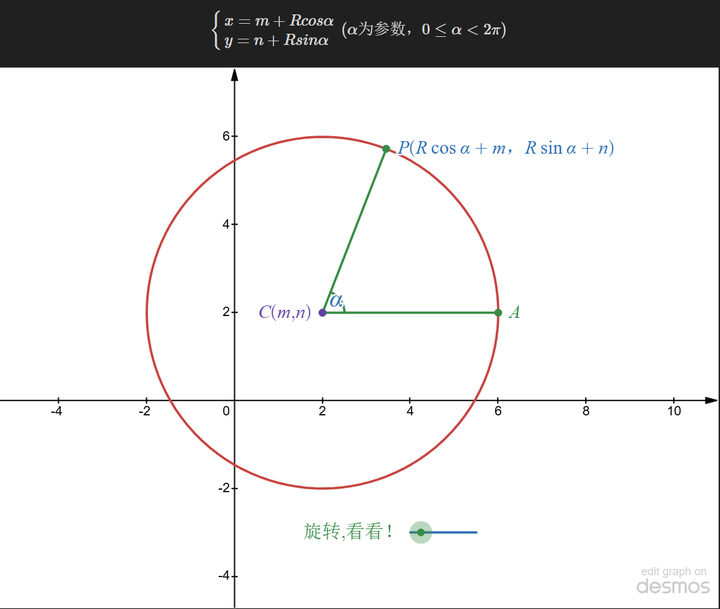 参数方程保持几何不变性,并且可以表示圆形等形状(其中一个 x 对应多个 y 值)。
参数方程保持几何不变性,并且可以表示圆形等形状(其中一个 x 对应多个 y 值)。
德卡斯特里奥
De Casteljau 算法是实际应用中用于评估和近似 Bézier 曲线以进行绘图和其他操作的方法。相比之前基于定义的评价方法,速度更快、更稳定,更接近Bézier曲线的特性。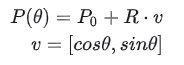
首先定义如下:
看上面的β。上标和下标有点混乱;可以用下面的三角递归来理解:
 上图中三角形的红边就是t0分割的两条线段的控制点。为了更形象地理解t0,P(t0)(即
上图中三角形的红边就是t0分割的两条线段的控制点。为了更形象地理解t0,P(t0)(即
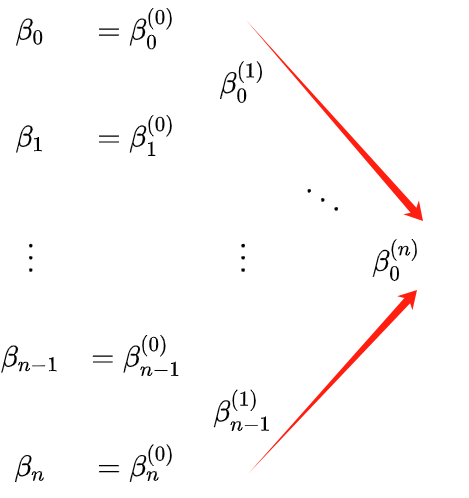
β00(n) ),两条曲线的控制点,可以参考下图: 上图展示了当t=0.5时各点之间的关系。 从“插值”的角度来看,计算过程也可以理解为:
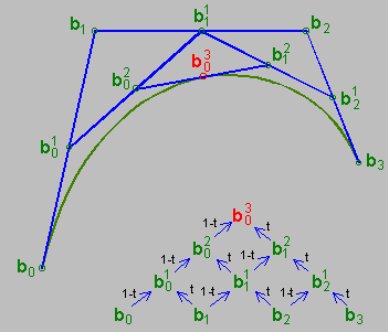 求每对相邻控制点的中点(因为t=0.5),即b01,b11,b21(请原谅我的记法;用LaTeX写太麻烦)
求每对相邻控制点的中点(因为t=0.5),即b01,b11,b21(请原谅我的记法;用LaTeX写太麻烦)
在b01−b11上求中点b02,在b11-b21上求中点b12
求 b02−b12 上的中点 b03 事实上,De Casteljau算法的本质就是插值和迭代。
- 基于 De Casteljau 的曲线绘制
- 目前观察到两种方法。
- 一种方法涉及以小步长增量将 t 从 0 遍历到 1(即0.01)。每次求 P(t) 时,都会使用递归公式来确定
β00(n) . 另一种方法是求P(t=0.5),然后对于两条划分曲线,分别求P(t=0.5)...这样的细分一直持续到曲线逼近为止。 执行 光看而不练习总感觉不真实。
于是我自己写了曲线绘制的实现代码,整理成一个工具包:Compilelife的Toolkit对应的核心代码在这里
-
 為什麼不````''{margin:0; }`始終刪除CSS中的最高邊距?在CSS 問題:不正確的代碼: 全球範圍將所有餘量重置為零,如提供的代碼所建議的,可能會導致意外的副作用。解決特定的保證金問題是更建議的。 例如,在提供的示例中,將以下代碼添加到CSS中,將解決餘量問題: body H1 { 保證金頂:-40px; } 此方法更精確,避免了由全局保證金重置...程式設計 發佈於2025-07-16
為什麼不````''{margin:0; }`始終刪除CSS中的最高邊距?在CSS 問題:不正確的代碼: 全球範圍將所有餘量重置為零,如提供的代碼所建議的,可能會導致意外的副作用。解決特定的保證金問題是更建議的。 例如,在提供的示例中,將以下代碼添加到CSS中,將解決餘量問題: body H1 { 保證金頂:-40px; } 此方法更精確,避免了由全局保證金重置...程式設計 發佈於2025-07-16 -
 為什麼我的CSS背景圖像出現?故障排除:CSS背景圖像未出現 ,您的背景圖像儘管遵循教程說明,但您的背景圖像仍未加載。圖像和样式表位於相同的目錄中,但背景仍然是空白的白色帆布。 而不是不棄用的,您已經使用了CSS樣式: bockent {背景:封閉圖像文件名:背景圖:url(nickcage.jpg); 如果您的html,cs...程式設計 發佈於2025-07-16
為什麼我的CSS背景圖像出現?故障排除:CSS背景圖像未出現 ,您的背景圖像儘管遵循教程說明,但您的背景圖像仍未加載。圖像和样式表位於相同的目錄中,但背景仍然是空白的白色帆布。 而不是不棄用的,您已經使用了CSS樣式: bockent {背景:封閉圖像文件名:背景圖:url(nickcage.jpg); 如果您的html,cs...程式設計 發佈於2025-07-16 -
 Python中何時用"try"而非"if"檢測變量值?使用“ try“ vs.” if”來測試python 在python中的變量值,在某些情況下,您可能需要在處理之前檢查變量是否具有值。在使用“如果”或“ try”構建體之間決定。 “ if” constructs result = function() 如果結果: 對於結果: ...程式設計 發佈於2025-07-16
Python中何時用"try"而非"if"檢測變量值?使用“ try“ vs.” if”來測試python 在python中的變量值,在某些情況下,您可能需要在處理之前檢查變量是否具有值。在使用“如果”或“ try”構建體之間決定。 “ if” constructs result = function() 如果結果: 對於結果: ...程式設計 發佈於2025-07-16 -
 找到最大計數時,如何解決mySQL中的“組函數\”錯誤的“無效使用”?如何在mySQL中使用mySql 檢索最大計數,您可能會遇到一個問題,您可能會在嘗試使用以下命令:理解錯誤正確找到由名稱列分組的值的最大計數,請使用以下修改後的查詢: 計數(*)為c 來自EMP1 按名稱組 c desc訂購 限制1 查詢說明 select語句提取名稱列和每個名稱...程式設計 發佈於2025-07-16
找到最大計數時,如何解決mySQL中的“組函數\”錯誤的“無效使用”?如何在mySQL中使用mySql 檢索最大計數,您可能會遇到一個問題,您可能會在嘗試使用以下命令:理解錯誤正確找到由名稱列分組的值的最大計數,請使用以下修改後的查詢: 計數(*)為c 來自EMP1 按名稱組 c desc訂購 限制1 查詢說明 select語句提取名稱列和每個名稱...程式設計 發佈於2025-07-16 -
 如何解決AppEngine中“無法猜測文件類型,使用application/octet-stream...”錯誤?appEngine靜態文件mime type override ,靜態文件處理程序有時可以覆蓋正確的mime類型,在錯誤消息中導致錯誤消息:“無法猜測mimeType for for file for file for [File]。 application/application/octet...程式設計 發佈於2025-07-16
如何解決AppEngine中“無法猜測文件類型,使用application/octet-stream...”錯誤?appEngine靜態文件mime type override ,靜態文件處理程序有時可以覆蓋正確的mime類型,在錯誤消息中導致錯誤消息:“無法猜測mimeType for for file for file for [File]。 application/application/octet...程式設計 發佈於2025-07-16 -
 FastAPI自定義404頁面創建指南response = await call_next(request) if response.status_code == 404: return RedirectResponse("https://fastapi.tiangolo.com") else: ...程式設計 發佈於2025-07-16
FastAPI自定義404頁面創建指南response = await call_next(request) if response.status_code == 404: return RedirectResponse("https://fastapi.tiangolo.com") else: ...程式設計 發佈於2025-07-16 -
 在Ubuntu/linux上安裝mysql-python時,如何修復\“ mysql_config \”錯誤?mysql-python安裝錯誤:“ mysql_config找不到”“ 由於缺少MySQL開發庫而出現此錯誤。解決此問題,建議在Ubuntu上使用該分發的存儲庫。使用以下命令安裝Python-MysqldB: sudo apt-get安裝python-mysqldb sudo pip in...程式設計 發佈於2025-07-16
在Ubuntu/linux上安裝mysql-python時,如何修復\“ mysql_config \”錯誤?mysql-python安裝錯誤:“ mysql_config找不到”“ 由於缺少MySQL開發庫而出現此錯誤。解決此問題,建議在Ubuntu上使用該分發的存儲庫。使用以下命令安裝Python-MysqldB: sudo apt-get安裝python-mysqldb sudo pip in...程式設計 發佈於2025-07-16 -
 如何從Python中的字符串中刪除表情符號:固定常見錯誤的初學者指南?從python import codecs import codecs import codecs 導入 text = codecs.decode('這狗\ u0001f602'.encode('utf-8'),'utf-8') 印刷(文字)#帶有...程式設計 發佈於2025-07-16
如何從Python中的字符串中刪除表情符號:固定常見錯誤的初學者指南?從python import codecs import codecs import codecs 導入 text = codecs.decode('這狗\ u0001f602'.encode('utf-8'),'utf-8') 印刷(文字)#帶有...程式設計 發佈於2025-07-16 -
 用戶本地時間格式及時區偏移顯示指南在用戶的語言環境格式中顯示日期/時間,並使用時間偏移在向最終用戶展示日期和時間時,以其localzone and格式顯示它們至關重要。這確保了不同地理位置的清晰度和無縫用戶體驗。以下是使用JavaScript實現此目的的方法。 方法:推薦方法是處理客戶端的Javascript中的日期/時間格式化和...程式設計 發佈於2025-07-16
用戶本地時間格式及時區偏移顯示指南在用戶的語言環境格式中顯示日期/時間,並使用時間偏移在向最終用戶展示日期和時間時,以其localzone and格式顯示它們至關重要。這確保了不同地理位置的清晰度和無縫用戶體驗。以下是使用JavaScript實現此目的的方法。 方法:推薦方法是處理客戶端的Javascript中的日期/時間格式化和...程式設計 發佈於2025-07-16 -
 Java中如何使用觀察者模式實現自定義事件?在Java 中創建自定義事件的自定義事件在許多編程場景中都是無關緊要的,使組件能夠基於特定的觸發器相互通信。本文旨在解決以下內容:問題語句我們如何在Java中實現自定義事件以促進基於特定事件的對象之間的交互,定義了管理訂閱者的類界面。 以下代碼片段演示瞭如何使用觀察者模式創建自定義事件: args...程式設計 發佈於2025-07-16
Java中如何使用觀察者模式實現自定義事件?在Java 中創建自定義事件的自定義事件在許多編程場景中都是無關緊要的,使組件能夠基於特定的觸發器相互通信。本文旨在解決以下內容:問題語句我們如何在Java中實現自定義事件以促進基於特定事件的對象之間的交互,定義了管理訂閱者的類界面。 以下代碼片段演示瞭如何使用觀察者模式創建自定義事件: args...程式設計 發佈於2025-07-16 -
 人臉檢測失敗原因及解決方案:Error -215錯誤處理:解決“ error:((-215)!empty()in Function Multultiscale中的“ openCV 要解決此問題,必須確保提供給HAAR CASCADE XML文件的路徑有效。在提供的代碼片段中,級聯分類器裝有硬編碼路徑,這可能對您的系統不准確。相反,OPENCV提...程式設計 發佈於2025-07-16
人臉檢測失敗原因及解決方案:Error -215錯誤處理:解決“ error:((-215)!empty()in Function Multultiscale中的“ openCV 要解決此問題,必須確保提供給HAAR CASCADE XML文件的路徑有效。在提供的代碼片段中,級聯分類器裝有硬編碼路徑,這可能對您的系統不准確。相反,OPENCV提...程式設計 發佈於2025-07-16 -
 為什麼不使用CSS`content'屬性顯示圖像?在Firefox extemers屬性為某些圖像很大,&& && && &&華倍華倍[華氏華倍華氏度]很少見,卻是某些瀏覽屬性很少,尤其是特定於Firefox的某些瀏覽器未能顯示圖像時未能顯示圖像時遇到了一個問題。這可以在提供的CSS類中看到:。 googlepic { 內容:url(&...程式設計 發佈於2025-07-16
為什麼不使用CSS`content'屬性顯示圖像?在Firefox extemers屬性為某些圖像很大,&& && && &&華倍華倍[華氏華倍華氏度]很少見,卻是某些瀏覽屬性很少,尤其是特定於Firefox的某些瀏覽器未能顯示圖像時未能顯示圖像時遇到了一個問題。這可以在提供的CSS類中看到:。 googlepic { 內容:url(&...程式設計 發佈於2025-07-16 -
 Go語言如何動態發現導出包類型?與反射軟件包中的有限類型的發現能力相反,本文探討了在運行時發現所有包裝類型(尤其是struntime go import( “ FMT” “去/進口商” ) func main(){ pkg,err:= incorter.default()。導入(“ time”) ...程式設計 發佈於2025-07-16
Go語言如何動態發現導出包類型?與反射軟件包中的有限類型的發現能力相反,本文探討了在運行時發現所有包裝類型(尤其是struntime go import( “ FMT” “去/進口商” ) func main(){ pkg,err:= incorter.default()。導入(“ time”) ...程式設計 發佈於2025-07-16 -
 為什麼在我的Linux服務器上安裝Archive_Zip後,我找不到“ class \” class \'ziparchive \'錯誤?Class 'ZipArchive' Not Found Error While Installing Archive_Zip on Linux ServerSymptom:When attempting to run a script that utilizes the ZipAr...程式設計 發佈於2025-07-16
為什麼在我的Linux服務器上安裝Archive_Zip後,我找不到“ class \” class \'ziparchive \'錯誤?Class 'ZipArchive' Not Found Error While Installing Archive_Zip on Linux ServerSymptom:When attempting to run a script that utilizes the ZipAr...程式設計 發佈於2025-07-16 -
 如何使用Python有效地以相反順序讀取大型文件?在python 反向行讀取器生成器 == ord('\ n'): 緩衝區=緩衝區[:-1] 剩餘_size- = buf_size lines = buffer.split('\ n'....程式設計 發佈於2025-07-16
如何使用Python有效地以相反順序讀取大型文件?在python 反向行讀取器生成器 == ord('\ n'): 緩衝區=緩衝區[:-1] 剩餘_size- = buf_size lines = buffer.split('\ n'....程式設計 發佈於2025-07-16
學習中文
- 1 走路用中文怎麼說? 走路中文發音,走路中文學習
- 2 坐飛機用中文怎麼說? 坐飞机中文發音,坐飞机中文學習
- 3 坐火車用中文怎麼說? 坐火车中文發音,坐火车中文學習
- 4 坐車用中文怎麼說? 坐车中文發音,坐车中文學習
- 5 開車用中文怎麼說? 开车中文發音,开车中文學習
- 6 游泳用中文怎麼說? 游泳中文發音,游泳中文學習
- 7 騎自行車用中文怎麼說? 骑自行车中文發音,骑自行车中文學習
- 8 你好用中文怎麼說? 你好中文發音,你好中文學習
- 9 謝謝用中文怎麼說? 谢谢中文發音,谢谢中文學習
- 10 How to say goodbye in Chinese? 再见Chinese pronunciation, 再见Chinese learning

























