簡單理解貝塞爾曲線。
想象一下,如果只能用直线、椭圆、圆,设计一辆线条流畅、外观复杂的汽车不是很困难吗?
1962年,法国工程师Pierre Bézier发表了贝塞尔曲线,最初用于汽车主体设计。
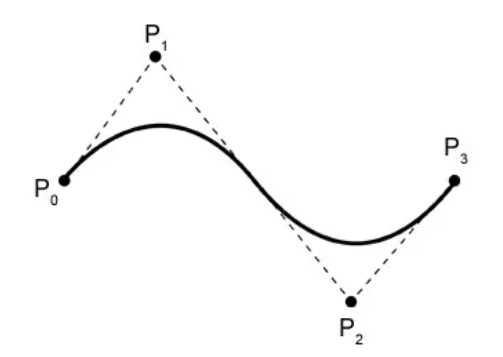
贝塞尔曲线可以通过一系列控制点定义一条平滑的曲线。曲线始终经过第一个和最后一个控制点,并受中间控制点形状的影响。此外,贝塞尔曲线具有凸包的属性。
贝塞尔曲线广泛应用于计算机图形和图像建模,例如动画、字体设计和工业设计。
公式
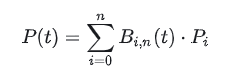
让我们了解一下。
P(t) 表示曲线上 t 处的点(t 是分数,取值范围为 0 到 1)。 t 处曲线上的点是什么?常见的曲线描述是:y = f(x),现在让我们将 P(t) 理解为 f(x)。不同的是,P(t)是参数表示(并且计算结果是[x,y]这样的“向量”),后面会详细解释
接下来,Pi表示第i个控制点(i从0开始)。以上图为例,有4个控制点,分别是P0、P1、P2、P3。公式中的n为控制点的最后一个索引,即n = 3(注意不是控制点的个数,而是计数减1)。
Bi,n(t) 是 Bernstein 基函数,也称为基函数。对于每个特定的(i,n),都有一个不同的基函数与之对应。如果从加权的角度理解,可以将基函数视为权重函数,表示第i个控制点Pi对t位置处的曲线坐标的“贡献”。
基函数的公式如下:
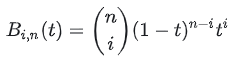
( in) 是组合数(从n中选择i有多少种方法?)。至于为什么基函数是这样的,可以结合De Casteljau算法来理解(见文中后面)
回到P(t)公式, Σi=0n 为求和符号,表示后续部分( i,n(t )⋅Pi ) 将从 i=0 到 i=n 求和。 以上图为例,假设我们要计算P(0.1),该怎么做呢?展开如下:
代入t=0.1得到:
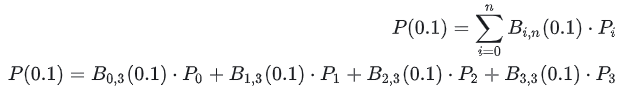
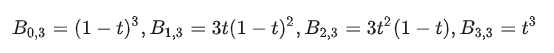 曲线的参数表示
曲线的参数表示
这里直接引用了网友的一篇文章(链接)
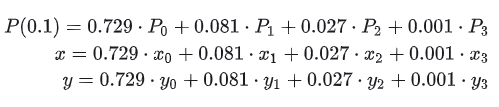
让我们重点关注上面的公式。
如上图所示,我们熟悉的直线可以从另一个角度来理解:用t(即|AP|从点P到已知点(x0,y0)的长度),那么通过上述三角函数就可以确定P点。
更一般的,可以写成: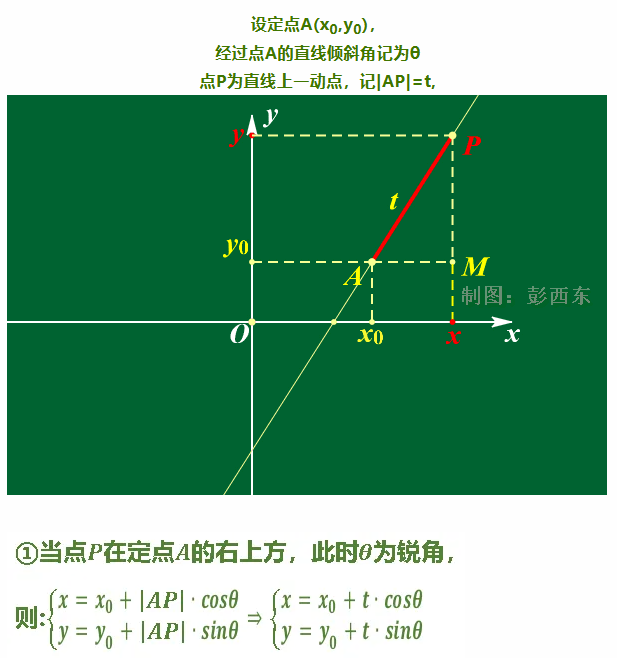
这里,P0是向量[x0,y0],v也是向量。加在一起时,P(t) 是向量 [x,y].
再看一下圆圈:
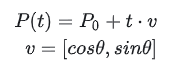
如图所示,圆可以看作有已知的圆心,圆上的任意点由旋转角度和半径确定。也可以写成:
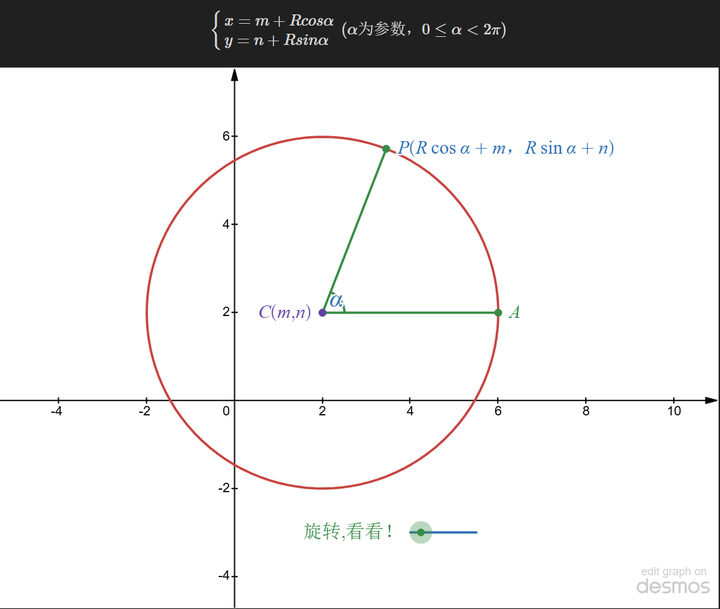 参数方程保持几何不变性,并且可以表示圆形等形状(其中一个 x 对应多个 y 值)。
参数方程保持几何不变性,并且可以表示圆形等形状(其中一个 x 对应多个 y 值)。
德卡斯特里奥
De Casteljau 算法是实际应用中用于评估和近似 Bézier 曲线以进行绘图和其他操作的方法。相比之前基于定义的评价方法,速度更快、更稳定,更接近Bézier曲线的特性。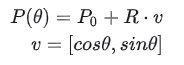
首先定义如下:
看上面的β。上标和下标有点混乱;可以用下面的三角递归来理解:
 上图中三角形的红边就是t0分割的两条线段的控制点。为了更形象地理解t0,P(t0)(即
上图中三角形的红边就是t0分割的两条线段的控制点。为了更形象地理解t0,P(t0)(即
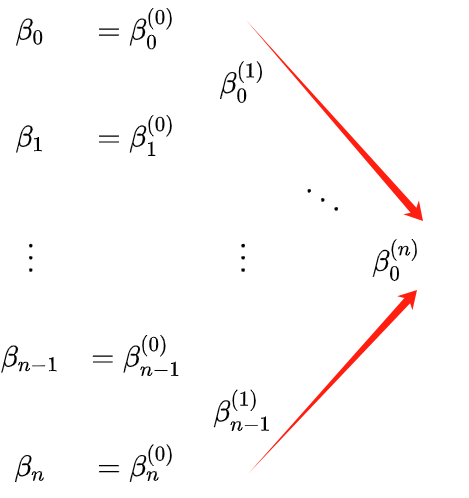
β00(n) ),两条曲线的控制点,可以参考下图: 上图展示了当t=0.5时各点之间的关系。 从“插值”的角度来看,计算过程也可以理解为:
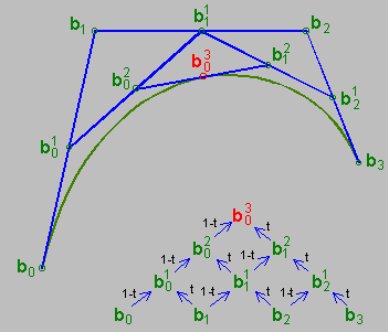 求每对相邻控制点的中点(因为t=0.5),即b01,b11,b21(请原谅我的记法;用LaTeX写太麻烦)
求每对相邻控制点的中点(因为t=0.5),即b01,b11,b21(请原谅我的记法;用LaTeX写太麻烦)
在b01−b11上求中点b02,在b11-b21上求中点b12
求 b02−b12 上的中点 b03 事实上,De Casteljau算法的本质就是插值和迭代。
- 基于 De Casteljau 的曲线绘制
- 目前观察到两种方法。
- 一种方法涉及以小步长增量将 t 从 0 遍历到 1(即0.01)。每次求 P(t) 时,都会使用递归公式来确定
β00(n) . 另一种方法是求P(t=0.5),然后对于两条划分曲线,分别求P(t=0.5)...这样的细分一直持续到曲线逼近为止。 执行 光看而不练习总感觉不真实。
于是我自己写了曲线绘制的实现代码,整理成一个工具包:Compilelife的Toolkit对应的核心代码在这里
-
 JavaScript計算兩個日期之間天數的方法How to Calculate the Difference Between Dates in JavascriptAs you attempt to determine the difference between two dates in Javascript, consider this s...程式設計 發佈於2025-07-13
JavaScript計算兩個日期之間天數的方法How to Calculate the Difference Between Dates in JavascriptAs you attempt to determine the difference between two dates in Javascript, consider this s...程式設計 發佈於2025-07-13 -
 Go語言如何動態發現導出包類型?與反射軟件包中的有限類型的發現能力相反,本文探索了替代方法,探索了在Runruntime。 go import( “ FMT” “去/進口商” ) func main(){ pkg,err:= incorter.default()。導入(“ time”) 如果er...程式設計 發佈於2025-07-13
Go語言如何動態發現導出包類型?與反射軟件包中的有限類型的發現能力相反,本文探索了替代方法,探索了在Runruntime。 go import( “ FMT” “去/進口商” ) func main(){ pkg,err:= incorter.default()。導入(“ time”) 如果er...程式設計 發佈於2025-07-13 -
 為什麼Microsoft Visual C ++無法正確實現兩台模板的實例?在Microsoft Visual C 中,Microsoft consions用戶strate strate strate strate strate strate strate strate strate strate strate strate strate strate strate st...程式設計 發佈於2025-07-13
為什麼Microsoft Visual C ++無法正確實現兩台模板的實例?在Microsoft Visual C 中,Microsoft consions用戶strate strate strate strate strate strate strate strate strate strate strate strate strate strate strate st...程式設計 發佈於2025-07-13 -
 為什麼使用固定定位時,為什麼具有100%網格板柱的網格超越身體?網格超過身體,用100%grid-template-columns 為什麼在grid-template-colms中具有100%的顯示器,當位置設置為設置的位置時,grid-template-colly修復了? 問題: 考慮以下CSS和html: class =“ snippet-code”> ...程式設計 發佈於2025-07-13
為什麼使用固定定位時,為什麼具有100%網格板柱的網格超越身體?網格超過身體,用100%grid-template-columns 為什麼在grid-template-colms中具有100%的顯示器,當位置設置為設置的位置時,grid-template-colly修復了? 問題: 考慮以下CSS和html: class =“ snippet-code”> ...程式設計 發佈於2025-07-13 -
 Python讀取CSV文件UnicodeDecodeError終極解決方法在試圖使用已內置的CSV模塊讀取Python中時,CSV文件中的Unicode Decode Decode Decode Decode decode Error讀取,您可能會遇到錯誤的錯誤:無法解碼字節 在位置2-3中:截斷\ uxxxxxxxx逃脫當CSV文件包含特殊字符或Unicode的路徑逃...程式設計 發佈於2025-07-13
Python讀取CSV文件UnicodeDecodeError終極解決方法在試圖使用已內置的CSV模塊讀取Python中時,CSV文件中的Unicode Decode Decode Decode Decode decode Error讀取,您可能會遇到錯誤的錯誤:無法解碼字節 在位置2-3中:截斷\ uxxxxxxxx逃脫當CSV文件包含特殊字符或Unicode的路徑逃...程式設計 發佈於2025-07-13 -
 如何有效地轉換PHP中的時區?在PHP 利用dateTime對象和functions DateTime對象及其相應的功能別名為時區轉換提供方便的方法。例如: //定義用戶的時區 date_default_timezone_set('歐洲/倫敦'); //創建DateTime對象 $ dateTime = ne...程式設計 發佈於2025-07-13
如何有效地轉換PHP中的時區?在PHP 利用dateTime對象和functions DateTime對象及其相應的功能別名為時區轉換提供方便的方法。例如: //定義用戶的時區 date_default_timezone_set('歐洲/倫敦'); //創建DateTime對象 $ dateTime = ne...程式設計 發佈於2025-07-13 -
 FastAPI自定義404頁面創建指南response = await call_next(request) if response.status_code == 404: return RedirectResponse("https://fastapi.tiangolo.com") else: ...程式設計 發佈於2025-07-13
FastAPI自定義404頁面創建指南response = await call_next(request) if response.status_code == 404: return RedirectResponse("https://fastapi.tiangolo.com") else: ...程式設計 發佈於2025-07-13 -
 `console.log`顯示修改後對象值異常的原因foo = [{id:1},{id:2},{id:3},{id:4},{id:id:5},],]; console.log('foo1',foo,foo.length); foo.splice(2,1); console.log('foo2', foo, foo....程式設計 發佈於2025-07-13
`console.log`顯示修改後對象值異常的原因foo = [{id:1},{id:2},{id:3},{id:4},{id:id:5},],]; console.log('foo1',foo,foo.length); foo.splice(2,1); console.log('foo2', foo, foo....程式設計 發佈於2025-07-13 -
 為什麼HTML無法打印頁碼及解決方案無法在html頁面上打印頁碼? @page規則在@Media內部和外部都無濟於事。 HTML:Customization:@page { margin: 10%; @top-center { font-family: sans-serif; font-weight: ...程式設計 發佈於2025-07-13
為什麼HTML無法打印頁碼及解決方案無法在html頁面上打印頁碼? @page規則在@Media內部和外部都無濟於事。 HTML:Customization:@page { margin: 10%; @top-center { font-family: sans-serif; font-weight: ...程式設計 發佈於2025-07-13 -
 為什麼我在Silverlight Linq查詢中獲得“無法找到查詢模式的實現”錯誤?查詢模式實現缺失:解決“無法找到”錯誤在銀光應用程序中,嘗試使用LINQ建立錯誤的數據庫連接的嘗試,無法找到以查詢模式的實現。 ”當省略LINQ名稱空間或查詢類型缺少IEnumerable 實現時,通常會發生此錯誤。 解決問題來驗證該類型的質量是至關重要的。在此特定實例中,tblpersoon可能...程式設計 發佈於2025-07-13
為什麼我在Silverlight Linq查詢中獲得“無法找到查詢模式的實現”錯誤?查詢模式實現缺失:解決“無法找到”錯誤在銀光應用程序中,嘗試使用LINQ建立錯誤的數據庫連接的嘗試,無法找到以查詢模式的實現。 ”當省略LINQ名稱空間或查詢類型缺少IEnumerable 實現時,通常會發生此錯誤。 解決問題來驗證該類型的質量是至關重要的。在此特定實例中,tblpersoon可能...程式設計 發佈於2025-07-13 -
 如何將多種用戶類型(學生,老師和管理員)重定向到Firebase應用中的各自活動?Red: How to Redirect Multiple User Types to Respective ActivitiesUnderstanding the ProblemIn a Firebase-based voting app with three distinct user type...程式設計 發佈於2025-07-13
如何將多種用戶類型(學生,老師和管理員)重定向到Firebase應用中的各自活動?Red: How to Redirect Multiple User Types to Respective ActivitiesUnderstanding the ProblemIn a Firebase-based voting app with three distinct user type...程式設計 發佈於2025-07-13 -
 人臉檢測失敗原因及解決方案:Error -215錯誤處理:解決“ error:((-215)!empty()in Function Multultiscale中的“ openCV 要解決此問題,必須確保提供給HAAR CASCADE XML文件的路徑有效。在提供的代碼片段中,級聯分類器裝有硬編碼路徑,這可能對您的系統不准確。相反,OPENCV提...程式設計 發佈於2025-07-13
人臉檢測失敗原因及解決方案:Error -215錯誤處理:解決“ error:((-215)!empty()in Function Multultiscale中的“ openCV 要解決此問題,必須確保提供給HAAR CASCADE XML文件的路徑有效。在提供的代碼片段中,級聯分類器裝有硬編碼路徑,這可能對您的系統不准確。相反,OPENCV提...程式設計 發佈於2025-07-13 -
 如何正確使用與PDO參數的查詢一樣?在pdo 中使用類似QUERIES在PDO中的Queries時,您可能會遇到類似疑問中描述的問題:此查詢也可能不會返回結果,即使$ var1和$ var2包含有效的搜索詞。錯誤在於不正確包含%符號。 通過將變量包含在$ params數組中的%符號中,您確保將%字符正確替換到查詢中。沒有此修改,PD...程式設計 發佈於2025-07-13
如何正確使用與PDO參數的查詢一樣?在pdo 中使用類似QUERIES在PDO中的Queries時,您可能會遇到類似疑問中描述的問題:此查詢也可能不會返回結果,即使$ var1和$ var2包含有效的搜索詞。錯誤在於不正確包含%符號。 通過將變量包含在$ params數組中的%符號中,您確保將%字符正確替換到查詢中。沒有此修改,PD...程式設計 發佈於2025-07-13 -
 如何從Python中的字符串中刪除表情符號:固定常見錯誤的初學者指南?從python import codecs import codecs import codecs 導入 text = codecs.decode('這狗\ u0001f602'.encode('utf-8'),'utf-8') 印刷(文字)#帶有...程式設計 發佈於2025-07-13
如何從Python中的字符串中刪除表情符號:固定常見錯誤的初學者指南?從python import codecs import codecs import codecs 導入 text = codecs.decode('這狗\ u0001f602'.encode('utf-8'),'utf-8') 印刷(文字)#帶有...程式設計 發佈於2025-07-13
學習中文
- 1 走路用中文怎麼說? 走路中文發音,走路中文學習
- 2 坐飛機用中文怎麼說? 坐飞机中文發音,坐飞机中文學習
- 3 坐火車用中文怎麼說? 坐火车中文發音,坐火车中文學習
- 4 坐車用中文怎麼說? 坐车中文發音,坐车中文學習
- 5 開車用中文怎麼說? 开车中文發音,开车中文學習
- 6 游泳用中文怎麼說? 游泳中文發音,游泳中文學習
- 7 騎自行車用中文怎麼說? 骑自行车中文發音,骑自行车中文學習
- 8 你好用中文怎麼說? 你好中文發音,你好中文學習
- 9 謝謝用中文怎麼說? 谢谢中文發音,谢谢中文學習
- 10 How to say goodbye in Chinese? 再见Chinese pronunciation, 再见Chinese learning

























