簡介1

函數呼叫自身的過程稱為遞歸，
對應的函數稱為遞歸函數.
由於電腦程式設計是數學的基本應用，因此讓
我們首先嘗試理解遞歸背後的數學推理。
一般來說，我們都知道函數的概念。簡而言之，函數是
提供輸入時產生輸出的數學方程式。例如：
假設函數 F(x) 是由下式定義的函數： F(x) = x^2 4
我們可以將此函數的 Java 程式碼編寫為：

公共靜態 int F(int x){
返回 (x * x 4);
}

現在，我們可以將 x 的不同值傳遞給該函數並接收我們的輸出
因此。
在繼續遞歸之前，讓我們試著理解另一個數學
稱為 數學歸納原理 (PMI) 的概念。

數學歸納原理 (PMI) 是一種證明陳述的技術，a
公式，或關於一組自然數的定理。它有
以下三步：
1.** 簡單案例的步驟*：在這一步驟中，我們將證明
所需的陳述 基本情況，例如 n = 0 或 n = 1。
2.* 假設步驟**：在這一步驟中，我們將假設所需的語句
對於 n = k 有效。

1. 證明步驟：根據假設步驟的結果，我們將證明， 只要 n = k 為真，n = k 1 對於所需方程式也成立。

例如：讓我們用數學歸納法證明：
S(N): 1 2 3 ... N = (N * (N 1))/2
(前N個自然數和)
證明：
步驟 1：當 N = 1 時，S(1) = 1 成立。
步驟 2：假設，對於 N = k，給定的陳述成立，即
1 2 3 .... k = (k * (k 1))/2
步驟 3：讓我們使用步驟 2 來證明 N = k 1 的陳述。

證明： 1 2 3 ... (k 1) = ((k 1)*(k 2))/2
證明：

將(k 1)加入步驟2所獲得的結果中的LHS與RHS：
1 2 3 ... (k 1) = (k*(k 1))/2 (k 1)

現在，從 RHS 端取 (k 1) common：
1 2 3 ... (k 1) = (k 1)*((k 2)/2)

根據我們試圖證明的說法：
1 2 3 ... (k 1) = ((k 1)*(k 2))/2
由此證明。

遞歸的工作

總結以上三點我們就可以定義遞歸方法的步驟了
步驟：
●基本情況：遞迴函數必須有一個終止條件，其中
該進程將停止呼叫自身。這種情況稱為基本情況。如果沒有基本情況，它將不斷調用自身並陷入
無限循環。很快，就會超出遞歸深度*，並且會拋出
錯誤。
●遞歸呼叫：遞歸函數將在較小的版本上呼叫自身
的主要問題。我們在編寫此步驟時需要小心
正確找出你的小問題是什麼至關重要。
●小計算：一般我們在每個遞歸
中執行一次計算步驟 稱呼。我們可以在遞歸呼叫之前或之後實現這個​​計算步驟
取決於問題的性質。

注意：遞歸使用儲存遞歸呼叫的內建堆疊。因此，
遞歸呼叫的次數必須盡可能少，以避免記憶體溢位。如果
遞歸呼叫次數超過最大允許數量，
**將超過遞歸深度**。
現在，讓我們看看如何使用遞歸解決一些常見問題

問題陳述 - 求一個數的階乘

方法：找出 PMI 的三個步驟，然後使用
將其關聯起來 遞迴

1. 歸納步驟：計算數字 n - F(n) 的階乘 歸納假設：我們已經得到了n-1 - F(n-1)
的階乘
2. 用F(n-1)表示F(n)：F(n)=n*F(n-1)。因此我們得到

public static int fact(int n){
int ans = 事實(n-1); #假設步驟
返回 ans * n; #從假設步驟解決問題
}

1. 代碼仍然不完整。缺少的部分是基本情況。現在我們將 試運轉以查找需要停止遞歸的情況。考慮 n = 5:

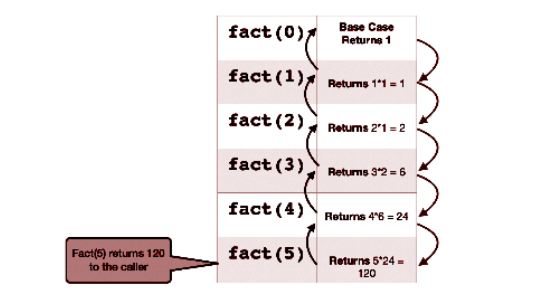
正如我們上面所看到的，我們已經知道n = 0的答案，即1。所以我們將
將此作為我們的基本情況。因此，程式碼現在變成：

公共靜態 int 階乘(int n){
if (n == 0) // 基本情況
返回 1;
別的
傳回 n*階乘(n-1); // 遞迴情況
}