k-最近鄰回歸

k-最近鄰（k-NN）迴歸是一種非參數方法，它根據特徵空間中 k 個最近鄰訓練資料點的平均值（或加權平均值）來預測輸出值。這種方法可以有效地對資料中的複雜關係進行建模，而無需假設特定的函數形式。

k-NN迴歸方法可以概括如下：

1. 距離度量：此演算法使用距離度量（通常為歐幾里德距離）來確定資料點的「接近度」。
2. k Neighbors：參數 k 指定在進行預測時要考慮多少個最近鄰居。
3. 預測：新資料點的預測值是其 k 個最近鄰點的值的平均值。

關鍵概念

1. 非參數化：與參數化模型不同，k-NN 不假設輸入特徵和目標變數之間的潛在關係的特定形式。這使得它可以靈活地捕捉複雜的模式。

2. 距離計算：距離度量的選擇可以顯著影響模型的表現。常見指標包括歐幾里德距離、曼哈頓距離和明可夫斯基距離。

3. k的選擇：可以基於交叉驗證來選擇鄰居的數量（k）。小 k 可能會導致過度擬合，而大 k 可能會過度平滑預測，可能導致欠擬合。

k-最近鄰迴歸範例

此範例示範如何使用具有多項式特徵的 k-NN 迴歸來建模複雜關係，同時利用 k-NN 的非參數性質。

Python 程式碼範例

1。導入庫

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, r2_score

此區塊匯入資料操作、繪圖和機器學習所需的庫。

2.產生樣本資料

np.random.seed(42)  # For reproducibility
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = 3 * X.ravel()   np.sin(2 * X.ravel()) * 5   np.random.normal(0, 1, 100)

此區塊產生表示與一些雜訊的關係的樣本數據，模擬真實世界的數據變化。

3.分割資料集

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

此區塊將資料集分為訓練集和測試集以進行模型評估。

4。創造多項式特徵

degree = 3  # Change this value for different polynomial degrees
poly = PolynomialFeatures(degree=degree)
X_poly_train = poly.fit_transform(X_train)
X_poly_test = poly.transform(X_test)

此區塊從訓練和測試資料集中產生多項式特徵，允許模型捕捉非線性關係。

5。建立並訓練 k-NN 迴歸模型

k = 5  # Number of neighbors
knn_model = KNeighborsRegressor(n_neighbors=k)
knn_model.fit(X_poly_train, y_train)

此區塊初始化 k-NN 迴歸模型並使用從訓練資料集導出的多項式特徵對其進行訓練。

6。做出預測

y_pred = knn_model.predict(X_poly_test)

此區塊使用經過訓練的模型對測試集進行預測。

7.繪製結果

plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', alpha=0.5, label='Data Points')
X_grid = np.linspace(0, 10, 1000).reshape(-1, 1)
X_poly_grid = poly.transform(X_grid)
y_grid = knn_model.predict(X_poly_grid)
plt.plot(X_grid, y_grid, color='red', linewidth=2, label=f'k-NN Regression (k={k}, Degree {degree})')
plt.title(f'k-NN Regression (Polynomial Degree {degree})')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()

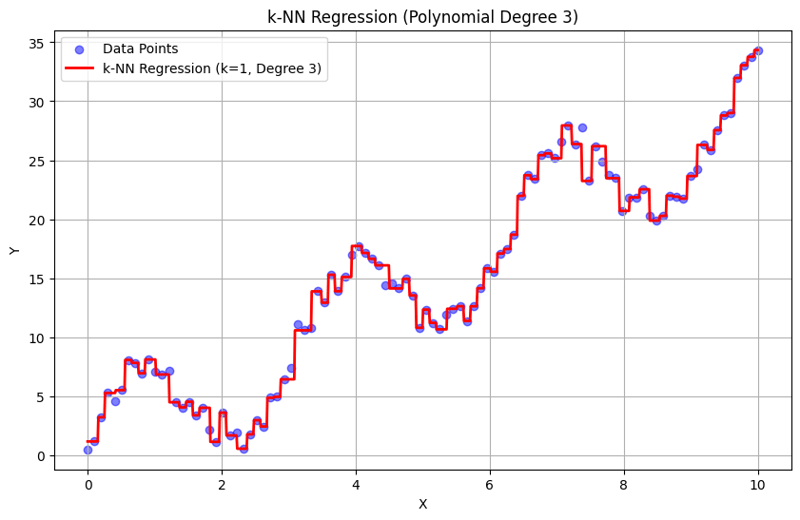
此區塊建立實際資料點與 k-NN 迴歸模型的預測值的散佈圖，並視覺化擬合曲線。

k = 1 時的輸出：

k = 10 時的輸出：

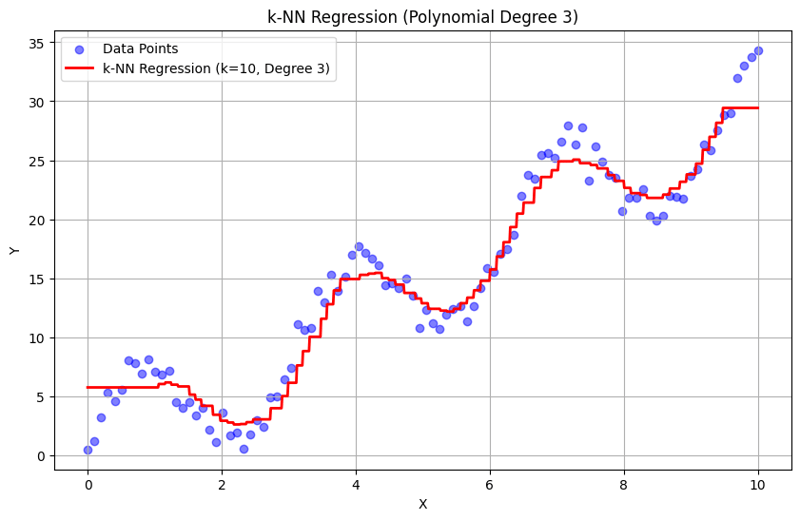
這種結構化方法演示瞭如何使用多項式特徵實現和評估 k 最近鄰回歸。透過對附近鄰居的反應進行平均來捕捉局部模式，k-NN 迴歸可以有效地對資料中的複雜關係進行建模，同時提供簡單的實作。 k 和多項式次數的選擇會顯著影響模型在捕捉潛在趨勢方面的表現和靈活性。