最大子數組問題及其歷史

20 世紀 70 年代末，瑞典數學家 Ulf Grenander 一直在討論一個問題：如何比暴力破解更有效地分析二維圖像數據數組？那時的電腦速度很慢，圖片相對於 RAM 來說也很大。更糟的是，在最壞的情況下，暴力破解需要 O(n^6) 時間（六次時間複雜度）。

首先，Grenandier 簡化了問題：給定一個一維數字數組，如何最有效地找到總和最大的連續子數組？

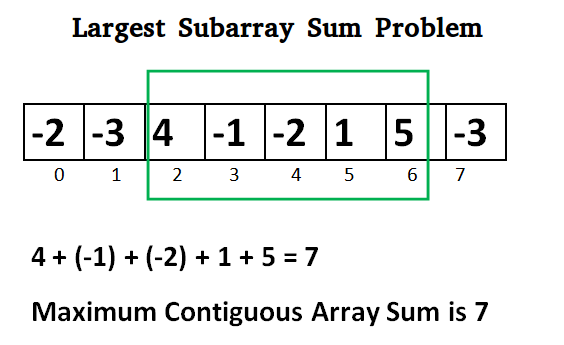
蠻力：一種具有立方時間複雜度的簡單方法

蠻力，分析一維數組的時間是分析二維數組的一半，因此檢查每種可能的組合（立方時間複雜度）需要 O(n^3)。

def max_subarray_brute_force(arr):
    max_sum = arr[0] # assumes arr has a length

    # iterate over all possible subarrays
    for i in range(len(arr)):
        for j in range(i, len(arr)):
            current_sum = 0
            # sum the elements of the subarray arr[i:j 1]
            for k in range(i, j   1):
                current_sum  = arr[k]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

print(max_subarray_brute_force([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

Grenander 的 O(n²) 優化：向前邁出了一步

Grenander 將其改進為 O(n^2) 解決方案。我在研究中找不到他的程式碼，但我的猜測是他只是擺脫了最內層的循環，該循環將兩個索引之間的所有數字相加。相反，我們可以在迭代子數組時保留運行總和，從而將循環次數從三個減少到兩個。

def max_subarray_optimized(arr):
    max_sum = arr[0]  # assumes arr has a length

    # iterate over all possible starting points of the subarray
    for i in range(len(arr)):
        current_sum = 0
        # sum the elements of the subarray starting from arr[i]
        for j in range(i, len(arr)):
            current_sum  = arr[j]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

Shamos 的分而治之：將問題分解為 O(n log n)

Grenander 向電腦科學家 Michael Shamos 展示了這個問題。 Shamos想了一個晚上，想出了一個分而治之的方法，O(n log n)。

這很聰明。其想法是將數組分成兩半，然後遞歸地找到每一半的最大子數組和以及穿過中點的子數組。

def max_crossing_sum(arr, left, mid, right):
    # left of mid
    left_sum = float('-inf')
    current_sum = 0
    for i in range(mid, left - 1, -1):
        current_sum  = arr[i]
        left_sum = max(left_sum, current_sum)

    # right of mid
    right_sum = float('inf')
    current_sum = 0
    for i in range(mid   1, right   1):
        current_sum  = arr[i]
        right_sum = max(right_sum, current_sum)

    # sum of elements on the left and right of mid, which is the maximum sum that crosses the midpoint
    return left_sum   right_sum

def max_subarray_divide_and_conquer(arr, left, right):
    # base case: only one element
    if left == right:
        return arr[left]

    # find the midpoint
    mid = (left   right) // 2

    # recursively find the maximum subarray sum for the left and right halves
    left_sum = max_subarray_divide_and_conquer(arr, left, mid)
    right_sum = max_subarray_divide_and_conquer(arr, mid   1, right)
    cross_sum = max_crossing_sum(arr, left, mid, right)

    # return the maximum of the three possible cases
    return max(left_sum, right_sum, cross_sum)

def max_subarray(arr):
    return max_subarray_divide_and_conquer(arr, 0, len(arr) - 1)


print(max_subarray([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

這將時間複雜度降低到 O(nlogn) 時間，因為首先將數組分為兩半 (O(logn))，然後找到最大交叉子數組需要 O(n)

Kadane 演算法：優雅的 O(n) 解決方案

統計學家 Jay Kadane 查看了代碼，立即發現 Shamos 的解決方案未能使用鄰接約束作為解決方案的一部分。

這就是他意識到的

-如果數組只有負數，那麼答案將始終是數組中最大的數字，假設我們不允許空子數組。

-如果數組只有正數，則答案總是將整個數組相加。

-如果你有一個同時包含正數和負數的數組，那麼你可以逐步遍歷該數組。如果在任何時候您正在查看的數字大於其之前的所有數字的總和，則解決方案不能包含任何先前的數字。因此，您從當前數字開始一個新的總和，同時追蹤迄今為止遇到的最大總和。

maxSubArray(nums):
    # avoiding type errors or index out of bounds errors
    if nums is None or len(nums) == 0:
        return 0


    max_sum = nums[0]  # max sum can't be smaller than any given element
    curr_sum = 0

    # Kadane's algorithm
    for num in nums:
        curr_sum = max(num, curr_sum   num)
        max_sum = max(curr_sum, max_sum)
    return max_sum

我喜歡這個演算法的原因是它可以應用於許多其他問題。試著調整它來解決這些 LeetCode 問題：

個和零
循環子數組的最大和
最小大小子數組和
最大升序子數組和
最大乘積子數組
連續子數組和
最大交替和子數組（高級）
矩形的最大和不大於 K