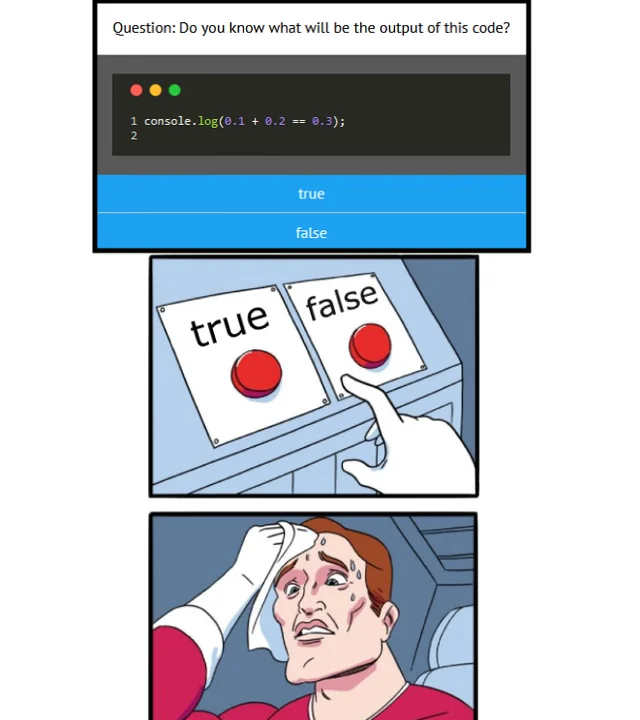
超越 JavaScript - 為什麼 + 在程式設計上不等於
當開發者第一次遇到這個看似令人費解的結果時,JavaScript 經常被嘲笑:
0.1 0.2 == 0.30000000000000004
關於 JavaScript 處理數字的迷因很普遍,常常導致許多人相信這種行為是該語言所獨有的。
然而,這個怪癖不僅限於 JavaScript。這是大多數程式語言處理浮點運算方式的結果。
例如,以下是來自 Java 和 Go 的程式碼片段,它們產生類似的結果:

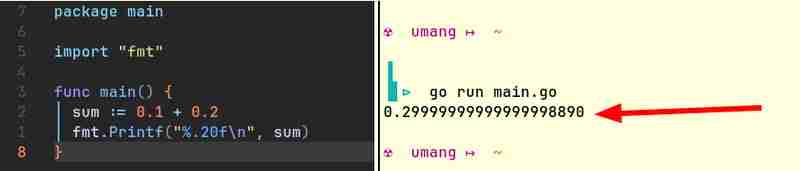
電腦本身只能儲存整數。他們不懂分數。 (他們會怎麼做?電腦進行算術運算的唯一方法是打開或關閉一些燈。燈可以打開或關閉。它不能「半」亮!)他們需要某種表示浮點數的方法。由於這種表示方法並不完全準確,因此 0.1 0.2 通常不等於 0.3。
所有分母由數係基數的質因數組成的分數都可以清晰地表達,而任何其他分數都會有重複的小數。例如,在以10 為基數的數字系統中,可以清楚地表示1/2、1/4、1/5、1/10 等分數,因為每種情況下的分母均由2 或5(10 的質因數)組成然而,像1/3、1/6、1/7 這樣的分數都有循環小數。
同樣,在二進位系統中,像 1/2、1/4、1/8 這樣的分數都可以清晰地表達,而所有其他分數都有循環小數。當您對這些循環小數執行算術運算時,您最終會得到剩餘的內容,當您將計算機的數字二進製表示形式轉換為人類可讀的以 10 為基數的表示形式時,這些剩餘內容會繼續存在。這就是導致大致正確結果的原因。
既然我們已經確定這個問題並非 JavaScript 所獨有,那麼讓我們探討一下浮點數是如何在幕後表示和處理的,以了解為什麼會出現這種行為。
為了了解浮點數在底層是如何表示和處理的,我們首先必須了解IEEE 754浮點標準。
IEEE 754 標準是廣泛使用的規範,用於在電腦系統中表示浮點數並對其執行算術運算。它的創建是為了確保在各種計算平台上使用浮點運算時的一致性。大多數程式語言和硬體實作(CPU、GPU 等)都遵守此標準。
這是數字在 IEEE 754 格式中的表示方式:
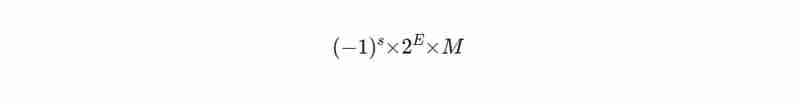
這裡s是符號位(0表示正數,1表示負數),M是尾數(保存數字的位數)和E 是決定數字小數位數的指數。
您將無法找到任何可以在此格式中精確表示數字(如 0.1、0.2 或 0.3)的 M 和 E 整數值。我們只能選擇給出最接近結果的 M 和 E 值。
這裡有一個工具,您可以用來確定 IEEE 754 十進制數表示法:https://www.h-schmidt.net/FloatConverter/IEEE754.html
IEEE 754 0.25 表示法:
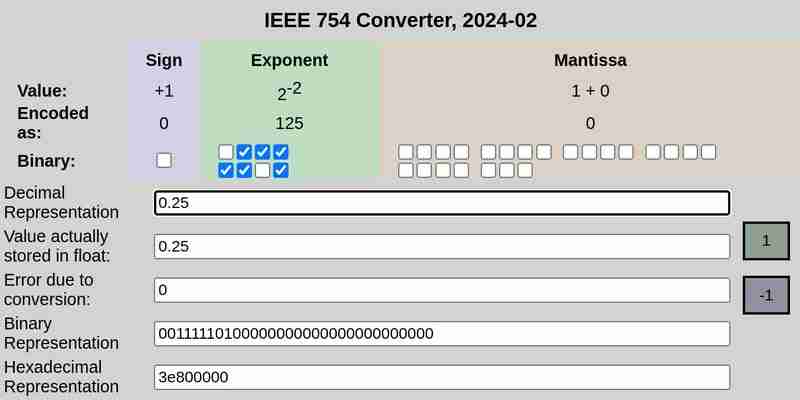
IEEE 754 分別表示 0.1 與 0.2:
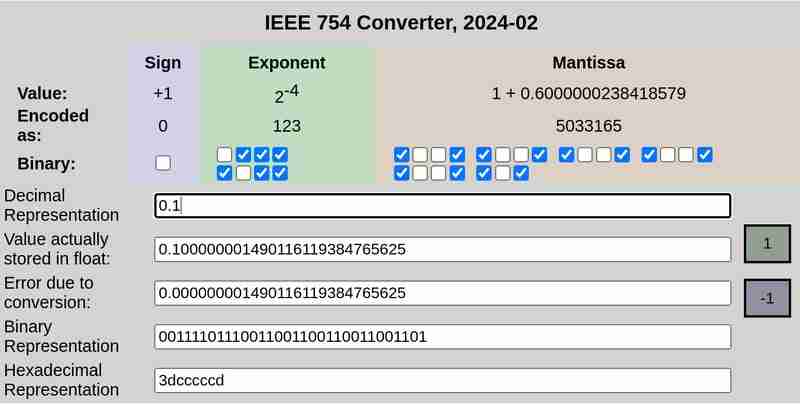
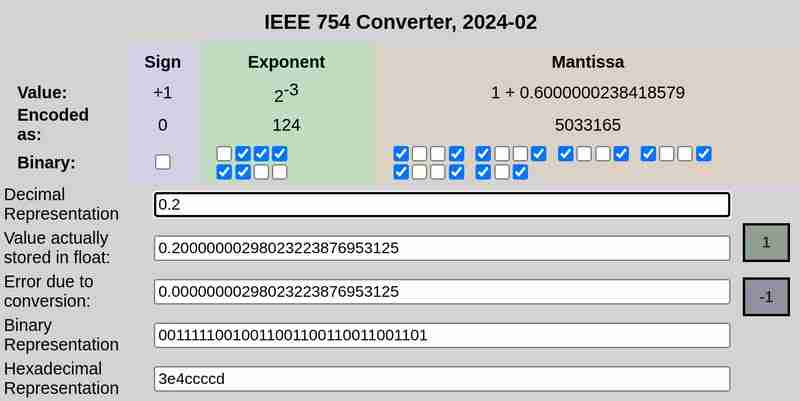
請注意,0.25時轉換誤差為0,而0.1和0.2則為非零誤差。
IEEE 754 定義了以下表示浮點數的格式:
單精確度(32 位元):1 位元符號,8 位元指數,23 位元尾數
雙精確度(64 位元):1 位元符號,11 位元指數,52 位元尾數
為了簡單起見,讓我們考慮使用 32 位元的單精度格式。
0.1的32位表示為:
0 01111011 10011001100110011001101
這裡第一位代表符號(0在本例中表示正數),接下來的8位(01111011)代表指數,最後23位(10011001100110011001101)代表尾數。
這不是準確的表示。它代表 ≈ 0.100000001490116119384765625
同樣,0.2的32位表示為:
0 01111100 10011001100110011001101
這也不是準確的表示。它代表 ≈ 0.20000000298023223876953125
加入後,結果是:
0 01111101 11001101010011001100110
十進位表示中的 ≈ 0.30000001192092896。
總之,看似令人困惑的結果 0.1 0.2 不產生 0.3 並不是 JavaScript 特有的異常現象,而是跨程式語言的浮點運算限制的結果。這種行為的根源在於數字的二進位表示形式,這在處理某些分數時本質上會導致精確度錯誤。
-
 如何在Java中正確顯示“ DD/MM/YYYY HH:MM:SS.SS”格式的當前日期和時間?如何在“ dd/mm/yyyy hh:mm:mm:ss.ss”格式“ gormat 解決方案: args)拋出異常{ 日曆cal = calendar.getInstance(); SimpleDateFormat SDF =新的SimpleDateFormat(“...程式設計 發佈於2025-04-09
如何在Java中正確顯示“ DD/MM/YYYY HH:MM:SS.SS”格式的當前日期和時間?如何在“ dd/mm/yyyy hh:mm:mm:ss.ss”格式“ gormat 解決方案: args)拋出異常{ 日曆cal = calendar.getInstance(); SimpleDateFormat SDF =新的SimpleDateFormat(“...程式設計 發佈於2025-04-09 -
 如何處理PHP文件系統功能中的UTF-8文件名?在PHP的Filesystem functions中處理UTF-8 FileNames 在使用PHP的MKDIR函數中含有UTF-8字符的文件很多flusf-8字符時,您可能會在Windows Explorer中遇到comploreer grounder grounder grounder gro...程式設計 發佈於2025-04-09
如何處理PHP文件系統功能中的UTF-8文件名?在PHP的Filesystem functions中處理UTF-8 FileNames 在使用PHP的MKDIR函數中含有UTF-8字符的文件很多flusf-8字符時,您可能會在Windows Explorer中遇到comploreer grounder grounder grounder gro...程式設計 發佈於2025-04-09 -
 如何在Java的全屏獨家模式下處理用戶輸入?在Java 中,以全屏幕獨立模式運行Java應用程序時,通常無法按期望的工作可能無法使用JAVA應用程序時,將用戶輸入在Java ProblemPassive rendering mode allows the use of KeyListener and ActionListener inter...程式設計 發佈於2025-04-09
如何在Java的全屏獨家模式下處理用戶輸入?在Java 中,以全屏幕獨立模式運行Java應用程序時,通常無法按期望的工作可能無法使用JAVA應用程序時,將用戶輸入在Java ProblemPassive rendering mode allows the use of KeyListener and ActionListener inter...程式設計 發佈於2025-04-09 -
 為什麼不````''{margin:0; }`始終刪除CSS中的最高邊距?在CSS 問題:不正確的代碼: 全球範圍將所有餘量重置為零,如提供的代碼所建議的,可能會導致意外的副作用。解決特定的保證金問題是更建議的。 例如,在提供的示例中,將以下代碼添加到CSS中,將解決餘量問題: body H1 { 保證金頂:-40px; } 此方法更精確,避免了由全局保證金重置...程式設計 發佈於2025-04-09
為什麼不````''{margin:0; }`始終刪除CSS中的最高邊距?在CSS 問題:不正確的代碼: 全球範圍將所有餘量重置為零,如提供的代碼所建議的,可能會導致意外的副作用。解決特定的保證金問題是更建議的。 例如,在提供的示例中,將以下代碼添加到CSS中,將解決餘量問題: body H1 { 保證金頂:-40px; } 此方法更精確,避免了由全局保證金重置...程式設計 發佈於2025-04-09 -
 如何將多種用戶類型(學生,老師和管理員)重定向到Firebase應用中的各自活動?Red: How to Redirect Multiple User Types to Respective ActivitiesUnderstanding the ProblemIn a Firebase-based voting app with three distinct user type...程式設計 發佈於2025-04-09
如何將多種用戶類型(學生,老師和管理員)重定向到Firebase應用中的各自活動?Red: How to Redirect Multiple User Types to Respective ActivitiesUnderstanding the ProblemIn a Firebase-based voting app with three distinct user type...程式設計 發佈於2025-04-09 -
 如何在JavaScript對像中動態設置鍵?在嘗試為JavaScript對象創建動態鍵時,如何使用此Syntax jsObj['key' i] = 'example' 1;不工作。正確的方法採用方括號: jsobj ['key''i] ='example'1; 在JavaScript中,數組是一...程式設計 發佈於2025-04-09
如何在JavaScript對像中動態設置鍵?在嘗試為JavaScript對象創建動態鍵時,如何使用此Syntax jsObj['key' i] = 'example' 1;不工作。正確的方法採用方括號: jsobj ['key''i] ='example'1; 在JavaScript中,數組是一...程式設計 發佈於2025-04-09 -
 為什麼我會收到MySQL錯誤#1089:錯誤的前綴密鑰?mySQL錯誤#1089:錯誤的前綴鍵錯誤descript [#1089-不正確的前綴鍵在嘗試在表中創建一個prefix鍵時會出現。前綴鍵旨在索引字符串列的特定前綴長度長度,可以更快地搜索這些前綴。 了解prefix keys `這將在整個Movie_ID列上創建標準主鍵。主密鑰對於唯一識...程式設計 發佈於2025-04-09
為什麼我會收到MySQL錯誤#1089:錯誤的前綴密鑰?mySQL錯誤#1089:錯誤的前綴鍵錯誤descript [#1089-不正確的前綴鍵在嘗試在表中創建一個prefix鍵時會出現。前綴鍵旨在索引字符串列的特定前綴長度長度,可以更快地搜索這些前綴。 了解prefix keys `這將在整個Movie_ID列上創建標準主鍵。主密鑰對於唯一識...程式設計 發佈於2025-04-09 -
 為什麼Microsoft Visual C ++無法正確實現兩台模板的實例?在Microsoft Visual C 中,Microsoft consions用戶strate strate strate strate strate strate strate strate strate strate strate strate strate strate strate st...程式設計 發佈於2025-04-09
為什麼Microsoft Visual C ++無法正確實現兩台模板的實例?在Microsoft Visual C 中,Microsoft consions用戶strate strate strate strate strate strate strate strate strate strate strate strate strate strate strate st...程式設計 發佈於2025-04-09 -
 如何將MySQL數據庫添加到Visual Studio 2012中的數據源對話框中?在Visual Studio 2012 儘管已安裝了MySQL Connector v.6.5.4,但無法將MySQL數據庫添加到實體框架的“ DataSource對話框”中。為了解決這一問題,至關重要的是要了解MySQL連接器v.6.5.5及以後的6.6.x版本將提供MySQL的官方Visual...程式設計 發佈於2025-04-09
如何將MySQL數據庫添加到Visual Studio 2012中的數據源對話框中?在Visual Studio 2012 儘管已安裝了MySQL Connector v.6.5.4,但無法將MySQL數據庫添加到實體框架的“ DataSource對話框”中。為了解決這一問題,至關重要的是要了解MySQL連接器v.6.5.5及以後的6.6.x版本將提供MySQL的官方Visual...程式設計 發佈於2025-04-09 -
 對象擬合:IE和Edge中的封面失敗,如何修復?To resolve this issue, we employ a clever CSS solution that solves the problem:position: absolute;top: 50%;left: 50%;transform: translate(-50%, -50%)...程式設計 發佈於2025-04-09
對象擬合:IE和Edge中的封面失敗,如何修復?To resolve this issue, we employ a clever CSS solution that solves the problem:position: absolute;top: 50%;left: 50%;transform: translate(-50%, -50%)...程式設計 發佈於2025-04-09 -
 找到最大計數時,如何解決mySQL中的“組函數\”錯誤的“無效使用”?如何在mySQL中使用mySql 檢索最大計數,您可能會遇到一個問題,您可能會在嘗試使用以下命令:理解錯誤正確找到由名稱列分組的值的最大計數,請使用以下修改後的查詢: 計數(*)為c 來自EMP1 按名稱組 c desc訂購 限制1 查詢說明 select語句提取名稱列和每個名稱...程式設計 發佈於2025-04-09
找到最大計數時,如何解決mySQL中的“組函數\”錯誤的“無效使用”?如何在mySQL中使用mySql 檢索最大計數,您可能會遇到一個問題,您可能會在嘗試使用以下命令:理解錯誤正確找到由名稱列分組的值的最大計數,請使用以下修改後的查詢: 計數(*)為c 來自EMP1 按名稱組 c desc訂購 限制1 查詢說明 select語句提取名稱列和每個名稱...程式設計 發佈於2025-04-09 -
 如何使用Java.net.urlConnection和Multipart/form-data編碼使用其他參數上傳文件?使用http request 上傳文件上傳到http server,同時也提交其他參數,java.net.net.urlconnection and Multipart/form-data Encoding是普遍的。 Here's a breakdown of the process:Mu...程式設計 發佈於2025-04-09
如何使用Java.net.urlConnection和Multipart/form-data編碼使用其他參數上傳文件?使用http request 上傳文件上傳到http server,同時也提交其他參數,java.net.net.urlconnection and Multipart/form-data Encoding是普遍的。 Here's a breakdown of the process:Mu...程式設計 發佈於2025-04-09 -
 如何實時捕獲和流媒體以進行聊天機器人命令執行?在開發能夠執行命令的chatbots的領域中,實時從命令執行實時捕獲Stdout,一個常見的需求是能夠檢索和顯示標準輸出(stdout)在cath cath cant cant cant cant cant cant cant cant interfaces in Chate cant inter...程式設計 發佈於2025-04-09
如何實時捕獲和流媒體以進行聊天機器人命令執行?在開發能夠執行命令的chatbots的領域中,實時從命令執行實時捕獲Stdout,一個常見的需求是能夠檢索和顯示標準輸出(stdout)在cath cath cant cant cant cant cant cant cant cant interfaces in Chate cant inter...程式設計 發佈於2025-04-09 -
 為什麼不使用CSS`content'屬性顯示圖像?在Firefox extemers屬性為某些圖像很大,&& && && &&華倍華倍[華氏華倍華氏度]很少見,卻是某些瀏覽屬性很少,尤其是特定於Firefox的某些瀏覽器未能在使用內容屬性引用時未能顯示圖像的情況。這可以在提供的CSS類中看到:。 googlepic { 內容:url(&...程式設計 發佈於2025-04-09
為什麼不使用CSS`content'屬性顯示圖像?在Firefox extemers屬性為某些圖像很大,&& && && &&華倍華倍[華氏華倍華氏度]很少見,卻是某些瀏覽屬性很少,尤其是特定於Firefox的某些瀏覽器未能在使用內容屬性引用時未能顯示圖像的情況。這可以在提供的CSS類中看到:。 googlepic { 內容:url(&...程式設計 發佈於2025-04-09
學習中文
- 1 走路用中文怎麼說? 走路中文發音,走路中文學習
- 2 坐飛機用中文怎麼說? 坐飞机中文發音,坐飞机中文學習
- 3 坐火車用中文怎麼說? 坐火车中文發音,坐火车中文學習
- 4 坐車用中文怎麼說? 坐车中文發音,坐车中文學習
- 5 開車用中文怎麼說? 开车中文發音,开车中文學習
- 6 游泳用中文怎麼說? 游泳中文發音,游泳中文學習
- 7 騎自行車用中文怎麼說? 骑自行车中文發音,骑自行车中文學習
- 8 你好用中文怎麼說? 你好中文發音,你好中文學習
- 9 謝謝用中文怎麼說? 谢谢中文發音,谢谢中文學習
- 10 How to say goodbye in Chinese? 再见Chinese pronunciation, 再见Chinese learning

























