本節介紹使用分治法找出最接近的點對的有效演算法。給定一組點，最近對問題是找到彼此最接近的兩個點。如下圖所示，繪製一條線來連接最近對動畫中兩個最近的點。

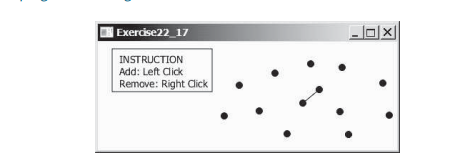
案例研究：找出最近的對，提出了一種用於尋找最近的點對的強力演算法。此演算法計算所有點對之間的距離並找到距離最小的點。顯然，該演算法需要 O(n^2) 時間。我們能否設計出更有效率的演算法？

我們將使用一種稱為分而治之的方法來解決這個問題。此方法將問題分成子問題，求解子問題，然後組合子問題的解以獲得整個問題的解。與動態規劃法不同，分而治之方法中的子問題不重疊。子問題就像原問題一樣，但規模較小，因此可以應用遞歸來解決問題。事實上，所有遞歸問題的解決方案都遵循分而治之的方法。

以下步驟說明如何使用分而治之的方法來解決最近配對問題。

• 第 1 步：依 x 座標升序對點進行排序。對於具有相同 x 座標的點，按 y 座標排序。這會產生一個排序的點列表 S。
• 步驟2：使用排序清單中的中點將S分成兩個大小相等的子集S1和S2。令中點位於 S1 處。遞歸地找到 S1 和 S2 中最接近的對。令 d1 和 d2 分別表示兩個子集中最近對的距離。
• 步驟3：找出S1中的點和S2中的點之間最接近的對，並將它們的距離表示為d3。最接近的一對是距離為 min(d1, d2, d3).

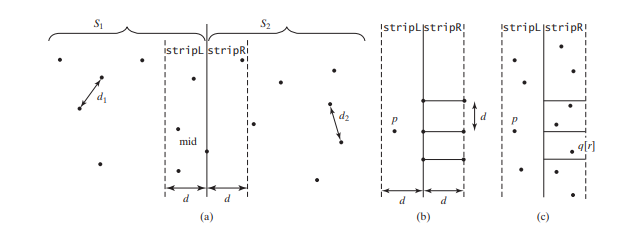
選擇排序需要 O(n^2) 時間。步驟 1 可以在 O(n log n) 時間內完成。步驟 3 可以在 O(n) 時間內完成。設 d = min(d1, d2)。我們已經知道最近的對距離不能大於 d。為了讓S1中的點和S2中的點形成S中最接近的對，左邊的點必須在stripL中，右邊的點在stripR中，如下圖所示（ A）。

對於stripL中的點p，只需考慮d X 2d矩形內的右點，如下(b)所示。矩形外的任何右點都不能與 p 形成最接近的對。由於S2中最近對的距離大於或等於d，因此最多可以有六個
矩形內的點。因此，對於stripL中的每個點，最多需要考慮stripR中的六個點。

對於stripL中的每個點p，如何定位stripR中對應的d X 2d矩形區域中的點？如果 stripL 和 stripR 中的點按其 y 座標的升序排序，則可以有效地完成此操作。令 pointsOrderedOnY 為按 y 座標升序排序的點列表。 pointsOrderedOnY可以在演算法中預先取得。 stripL 和 stripR 可以從步驟 3 中的 pointsOrderedOnY 取得，如下面的程式碼所示。

對於pointsOrderedOnY 中的每個點p
if (p 在 S1 且 mid.x – p.x 將 p 附加到 stripL;
else if (p 在 S2 且 p.x - mid.x 將 p 附加到 stripR;

設stripL和stripR中的點為{p0, p1, ... , pk}和{q0, q1, ... , qt}，如圖上圖(c)。 stripL 中的點與 stripR 中的點之間最接近的對可以使用下面程式​​碼中描述的演算法找到。

d = min(d1, d2);
 r = 0; // r is the index of a point in stripR
 for (each point p in stripL) {
 // Skip the points in stripR below p.y - d
  while (r 



stripL中的點依 p0, p1, ... , pk 的順序考慮。對於 stripL 中的點 p，跳過 stripR 中 p.y – d 下方的點（第 5-6 行）。一旦跳過某個點，就不再考慮該點。 while 循環（第 9-17 行）檢查 (p, q[r1]) 是否是可能最接近的對。這樣的 q[r1] 對最多有 6 個，因為 stripR 中兩點之間的距離不能小於 d。因此，在步驟 3 中找到最接近的對的複雜度是 O(n).

請注意，上述步驟中的步驟 1 僅執行一次以對點進行預先排序。假設所有點都已預先排序。令 T(n) 表示該演算法的時間複雜度。因此，



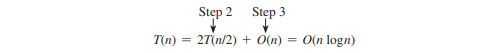
因此，可以在 O(n log n) 時間內找到最接近的點對。