本節給出了幾個確定重複、序列和選擇語句的 Big O 的例子。

實施例1

考慮以下循環的時間複雜度：

for (int i = 1; i k = k 5;
}

這是一個常數時間，c，用於執行

k = k 5;

由於循環執行了n次，所以循環的時間複雜度為

T(n) = (常數 c)*n = O(n).

理論分析預測了演算法的性能。為了了解演算法的執行情況，我們執行下面程式中的程式碼來取得 n = 1000000、10000000、100000000 和 100000000 時的執行時間。

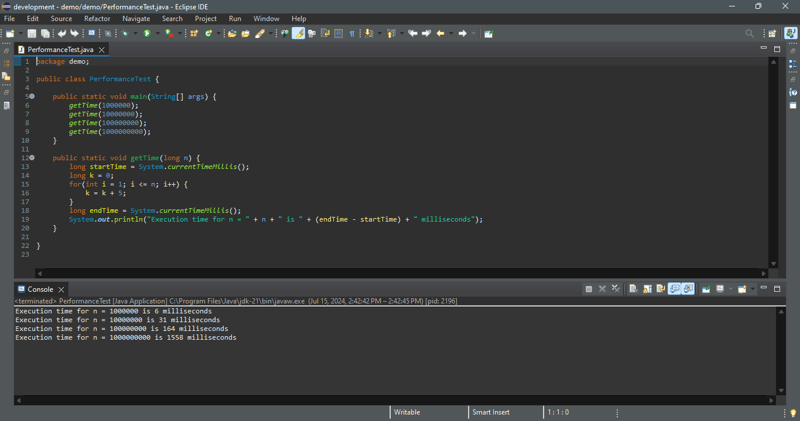
我們的分析預測了該循環的線性時間複雜度。如範例輸出所示，當輸入大小增加 10 倍時，運行時間約增加 10 倍。執行結果證實了預測。

實施例2

以下循環的時間複雜度為何？

for (int i = 1; i for (int j = 1; j k = k i j;
}
}

這是一個常數時間，c，用於執行

k = k i j;

外循環執行n次。對於外循環中的每次迭代，內循環都會執行 n 次。因此，循環的時間複雜度為

T(n) = (常數 c)*n*n = O(n^2)

時間複雜度為 O(n^2) 的演算法稱為二次演算法，它表現出二次成長率。隨著問題規模的增加，二次演算法會快速成長。如果將輸入大小加倍，演算法的時間就會增加四倍。具有嵌套循環的演算法通常是二次的。

實施例3

考慮以下循環：

for (int i = 1; i for (int j = 1; j k = k i j;
}
}

外循環執行n次。對於 i = 1, 2, c ，內循環執行一次、兩次和 n 次。因此，循環的時間複雜度為

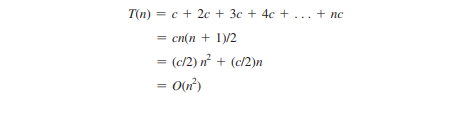
實施例4

考慮以下循環：

for (int i = 1; i for (int j = 1; j k = k i j;
}
}

內循環執行20次，外循環執行n次。因此，循環的時間複雜度為

T(n) = 20*c*n = O(n)

實施例5

考慮以下序列：

for (int j = 1; j k = k 4;
}

for (int i = 1; i for (int j = 1; j k = k i j;
}
}

第一個迴圈執行10次，第二個迴圈執行20 * n次。因此，循環的時間複雜度為

T(n) = 10*c 20*c*n = O(n)

實施例6

考慮以下選擇語句：

if (list.contains(e)) {
System.out.println(e);
}
別的
for (物件 t: 列表) {
System.out.println(t);
}

假設清單包含n個元素。 list.contains(e) 的執行時間為 O(n)。 else 子句中的迴圈需要 O(n) 時間。因此，整個語句的時間複雜度為

實施例7

考慮整數 n 的 a^n 計算。一個簡單的演算法將 a 乘以 n 次，如下所示：

結果 = 1;
for (int i = 1; i 結果*=a;

此演算法需要 O(n) 時間。不失一般性，假設 n = 2^k。您可以使用以下方案改進演算法：

結果 = a;
for (int i = 1; i 結果 = 結果 * 結果;

此演算法需要 O(logn) 時間。對於任意的n，可以修改演算法，證明複雜度仍然是O(logn)。

為了簡單起見，由於 0(logn) = 0(log2n) = 0(logan)，所以省略了常數基數。