图的深度优先搜索从图中的一个顶点开始，在回溯之前尽可能访问图中的所有顶点。
图的深度优先搜索类似于树遍历，树遍历中讨论的树的深度优先搜索。对于树，搜索从根开始。在图中，搜索可以从任何顶点开始。

树的深度优先搜索首先访问根，然后递归访问根的子树。类似地，图的深度优先搜索首先访问一个顶点，然后递归地访问与该顶点相邻的所有顶点。不同之处在于该图可能包含循环，这可能导致无限递归。为了避免这个问题，你需要跟踪已经访问过的顶点。

该搜索被称为深度优先，因为它尽可能在图中搜索“更深”。搜索从某个顶点 v 开始。访问完 v 后，它会访问 v 的未访问的邻居。如果 v 没有未访问的邻居，则搜索回溯到到达 v 的顶点。我们假设图是连通的，并且搜索开始从任意顶点出发都可以到达所有顶点。

深度优先搜索算法

深度优先搜索的算法在下面的代码中描述。

输入：G = (V, E) 和起始顶点 v
输出：以 v
为根的 DFS 树 1 树 dfs(顶点 v) {
2 访问 v；
3 对于 v
的每个邻居 w 4 if (w尚未被访问过) {
5 将 v 设置为树中 w 的父级；
6 dfs(w);
7 }
8 }

可以使用名为isVisited的数组来表示某个顶点是否已被访问。最初，对于每个顶点 i，isVisited[i] 为 false。一旦访问了某个顶点（例如 v），isVisited[v] 就会设置为 true。

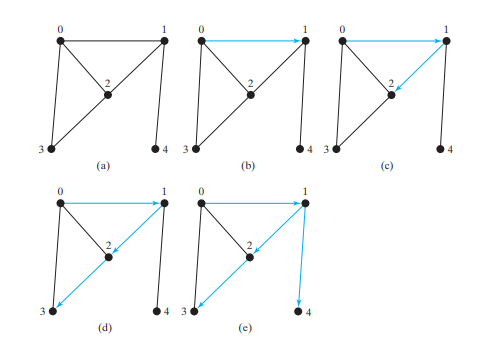
考虑下图 (a) 中的图表。假设我们从顶点 0 开始深度优先搜索。首先访问 0，然后访问它的任何邻居，比如 1。现在访问 1，如下图 (b) 所示。顶点 1 有 3 个邻居：0、2 和 4。由于 0 已经被访问过，因此您将访问 2 或 4。让我们选择 2。现在 2 被访问，如下图 (c) 所示。顶点 2 有 3 个邻居：0、1 和 3。由于 0 和 1 已经被访问过，所以选择 3。现在访问 3，如下图 (d) 所示。至此，顶点已按以下顺序被访问过：

0、1、2、3

由于3的所有邻居都被访问过，所以回溯到2。由于2的所有顶点都被访问过，所以回溯到1。4与1相邻，但4还没有被访问过。因此，访问4，如下图(e)所示。由于 4 的所有邻居都已访问过，因此回溯到 1。
由于1的所有邻居都被访问过，所以回溯到0。因为0的所有邻居都被访问过，所以搜索结束。

由于每条边和每个顶点仅被访问一次，因此dfs方法的时间复杂度为O(|E| |V|)，其中|E | 表示边数，|V| 表示顶点数。

深度优先搜索的实现

上面代码中的DFS算法使用了递归。很自然地使用递归来实现它。或者，您可以使用堆栈。

dfs(int v)方法在AbstractGraph.java的第164-193行实现。它返回 Tree 类的实例，以顶点 v 作为根。该方法将搜索到的顶点存储在列表 searchOrder（第 165 行）中，每个顶点的父级存储在数组 parent（第 166 行）中，并使用 isVisited 数组来指示是否已访问顶点（第 171 行）。它调用辅助方法 dfs(v, Parent, searchOrder, isVisited) 执行深度优先搜索（第 174 行）。

在递归辅助方法中，搜索从顶点u开始。 u 被添加到第 184 行的 searchOrder 中，并被标记为已访问（第 185 行）。对于 u 的每个未访问的邻居，递归调用该方法来执行深度优先搜索。当访问顶点 e.v 时，e.v 的父顶点存储在 parent[e.v] 中（第 189 行）。当访问连通图或连通组件中的所有顶点时，该方法返回。

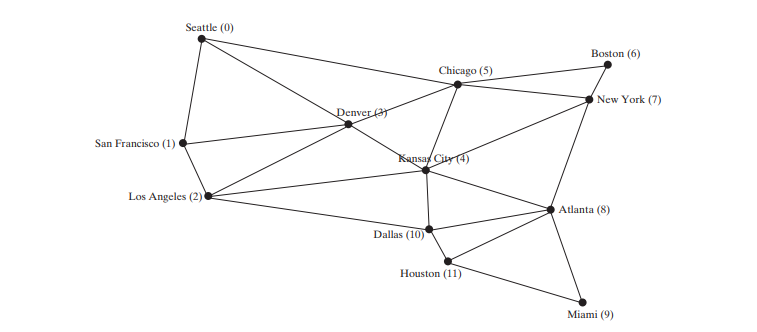
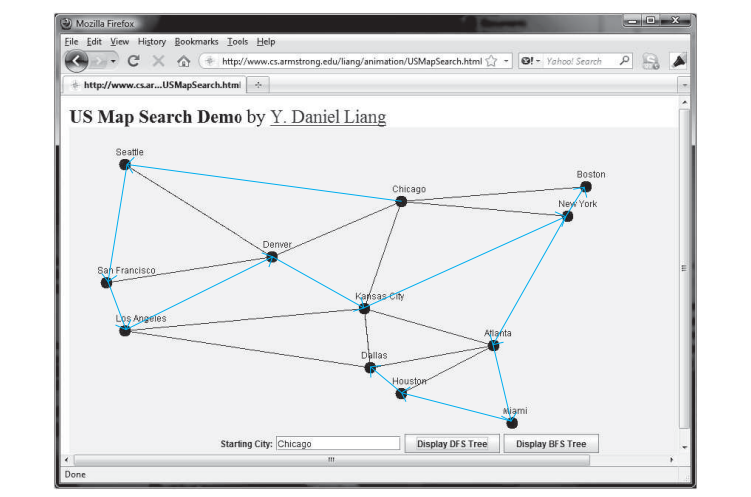
下面的代码给出了一个测试程序，该程序显示上图中从芝加哥开始的图形的 DFS。从芝加哥出发的DFS示意图如下图所示。

public class TestDFS {

    public static void main(String[] args) {
        String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1}, {0, 3}, {0, 5},
                {1, 0}, {1, 2}, {1, 3},
                {2, 1}, {2, 3}, {2, 4}, {2, 10},
                {3, 0}, {3, 1}, {3, 2}, {3, 4}, {3, 5},
                {4, 2}, {4, 3}, {4, 5}, {4, 7}, {4, 8}, {4, 10},
                {5, 0}, {5, 3}, {5, 4}, {5, 6}, {5, 7},
                {6, 5}, {6, 7},
                {7, 4}, {7, 5}, {7, 6}, {7, 8},
                {8, 4}, {8, 7}, {8, 9}, {8, 10}, {8, 11},
                {9, 8}, {9, 11},
                {10, 2}, {10, 4}, {10, 8}, {10, 11},
                {11, 8}, {11, 9}, {11, 10}
        };

        Graph graph = new UnweightedGraph(vertices, edges);
        AbstractGraph.Tree dfs = graph.dfs(graph.getIndex("Chicago"));

        java.util.List searchOrders = dfs.getSearchOrder();
        System.out.println(dfs.getNumberOfVerticesFound()   " vertices are searched in this DFS order:");
        for(int i = 0; i 



按此 DFS 顺序搜索 12 个顶点：

 芝加哥 西雅图 旧金山 洛杉矶 丹佛

 堪萨斯城 纽约 波士顿 亚特兰大 迈阿密 休斯顿 达拉斯

西雅图的父级是芝加哥

旧金山的父级是西雅图

洛杉矶的父级是旧金山

丹佛的父级是洛杉矶

堪萨斯城的母公司是丹佛

波士顿的父级是纽约

纽约的父级是堪萨斯城

亚特兰大的父级是纽约

迈阿密的父级是亚特兰大

达拉斯的父母是休斯顿

休斯顿的父母是迈阿密




  
  
  DFS的应用


深度优先搜索可以用来解决很多问题，例如：

检测图是否连通。从任意顶点开始搜索图。如果搜索到的顶点数与图中的顶点数相同，则该图是连通的。否则，图形不连通。
检测两个顶点之间是否存在路径。
寻找两个顶点之间的路径。
查找所有连接的组件。连通分量是最大连通子图，其中每对顶点都通过路径连接。
检测图中是否存在环路。
在图中找到一个循环。
寻找哈密顿路径/循环。图中的哈密顿路径是只访问图中每个顶点一次的路径。 哈密尔顿循环访问图中的每个顶点一次并返回到起始顶点。
前六个问题可以使用AbstractGraph.java中的dfs方法轻松解决。要找到哈密顿路径/循环，您必须探索所有可能的 DFS，以找到通向最长路径的路径。哈密​​顿路径/循环有很多应用，包括解决著名的骑士之旅问题。