Введение 1

Процесс, в котором функция вызывает саму себя, называется рекурсией, а
соответствующая функция называется рекурсивной функцией.
Поскольку компьютерное программирование является фундаментальным применением математики, пусть
сначала попытаемся понять математическую основу рекурсии.
В общем, всем нам знакомо понятие функции. В двух словах, функции — это
математические уравнения, которые производят выходные данные при предоставлении входных данных. Например:
Предположим, что функция F(x) — это функция, определяемая следующим образом: F(x) = x^2 4
Мы можем написать код Java для этой функции как:

public static int F(int x){
возврат (х * х 4);
}

Теперь мы можем передавать в эту функцию разные значения x и получать результат
соответственно.
Прежде чем перейти к рекурсии, давайте попробуем разобраться в еще одной математической
концепция, известная как Принцип математической индукции (PMI).

Принцип математической индукции (PMI) — это метод доказательства утверждения,
формула или теорема, утверждаемая о множестве натуральных чисел. Он имеет
следующие три шага:
1.** Шаг тривиального случая*: На этом шаге мы докажем искомое утверждение для
базовый случай, например n = 0 или n = 1.
2.* Шаг предположения**: на этом этапе мы предполагаем, что желаемое утверждение
справедливо для n = k.

1. Шаг доказательства: На основании результатов шага предположения мы докажем, что n = k 1 также верно для искомого уравнения, если n = k истинно.

Например: давайте докажем, используя принцип математической индукции, что:
S(N): 1 2 3 ... N = (N * (N 1))/2
(Сумма первых N натуральных чисел)
Доказательство:
Шаг 1: Для N = 1 верно S(1) = 1.
Шаг 2: Предположим, что данное утверждение верно для N = k, т. е.
1 2 3 .... k = (k * (k 1))/2
Шаг 3. Докажем утверждение для N = k 1, используя шаг 2.

Чтобы доказать: 1 2 3 ... (k 1) = ((k 1)*(k 2))/2
Доказательство:

Добавление (k 1) к левой и правой части результата, полученного на шаге 2:
1 2 3 ... (к 1) = (к*(к 1))/2 (к 1)

Теперь, беря (k 1) общее с правой стороны:
1 2 3 ... (к 1) = (к 1)*((к 2)/2)

Согласно утверждению, которое мы пытаемся доказать:
1 2 3 ... (к 1) = ((к 1)*(к 2))/2
Следовательно, доказано.

Работа рекурсии

Мы можем определить этапы рекурсивного подхода, суммируя три приведенных выше
шаги:
● Базовый случай: рекурсивная функция должна иметь завершающее условие, при котором
процесс перестанет вызывать себя. Такой случай известен как базовый случай. Без базового варианта он будет продолжать вызывать сам себя и застревать в
бесконечный цикл. Вскоре глубина рекурсии* будет превышена и будет выброшено
ошибка.
● Рекурсивный вызов: рекурсивная функция вызывает себя в уменьшенной версии
основной проблемы. Нам нужно быть осторожными при написании этого шага
крайне важно правильно понять, в чем заключается ваша меньшая проблема.
● Небольшой расчет. Обычно мы выполняем шаг расчета в каждом рекурсивном
вызов. Мы можем выполнить этот шаг вычисления до или после рекурсивного вызова
в зависимости от характера проблемы.

Примечание: Рекурсия использует встроенный стек, в котором хранятся рекурсивные вызовы. Следовательно,
количество рекурсивных вызовов должно быть как можно меньшим, чтобы избежать переполнения памяти. Если
количество вызовов рекурсии превышает максимально допустимое количество,
**глубина рекурсии** будет превышена.
Теперь давайте посмотрим, как решить несколько распространенных проблем с помощью рекурсии

Постановка задачи. Найти факториал числа

Подход: определение трех этапов PMI, а затем их связь с помощью
рекурсия

1. Шаг индукции: вычисление факториала числа n - F(n) Гипотеза индукции: мы уже получили факториал n-1 - F(n-1)
2. Выражая F(n) через F(n-1): F(n)=n*F(n-1). Таким образом, мы получаем

public static int fact(int n){
int ans = факт (n-1); #Успенский шаг
вернуть ответ * n; #Решение проблемы на этапе предположения
}

1. Код еще не завершен. Недостающая часть — это базовый вариант. Теперь мы будем пробный прогон, чтобы найти случай, когда рекурсию необходимо остановить. Рассмотрим n = 5:

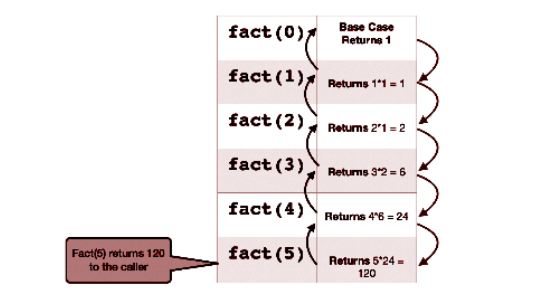
Как мы видим выше, мы уже знаем ответ для n = 0, то есть 1. Итак, мы
оставьте это как наш базовый вариант. Следовательно, код теперь выглядит следующим образом:

public static int Factorial(int n){
if (n == 0) // базовый случай
вернуть 1;
еще
вернуть n*факториал(n-1); // рекурсивный случай
}