Очередь

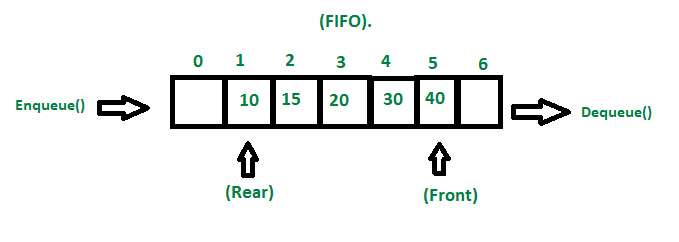
Очереди, которые часто изучают вместе со стеками, также представляют собой абстрактные типы данных, которые определяются в терминах операций, которые мы в них выполняем. Большая разница между стеками и очередями заключается в порядке операций, которые они реализуют, очереди — ПЕРВЫЙ ВХОД, ПЕРВЫЙ ВЫХОД, или FIFO, это означает, что первое, что попадает в очередь, первым выходит наружу, а стеки — ПОСЛЕДНИМ ВХОДОМ. ПЕРВЫМ, поэтому последнее, что мы поместим, будет первым, что мы получим обратно

Очереди определяются тремя операциями:

• поставить в очередь (поместить элемент в конец очереди)
• удалить из очереди (взять элемент из начала очереди)
• просмотреть (получить первый элемент, не удаляя его из очереди)

Мы можем думать об очередях как о очередях в ресторане: когда мы встаем в очередь, нам приходится ждать, пока все, кто стоит перед нами, будут обслужены, прежде чем придет наше время.

Выполнение

Вот простая реализация очереди с использованием массива:

#include 
#include 
#include 

#define QUEUE_LEN 1024

struct queue_t {
    uint32_t data[QUEUE_LEN];
    size_t ptr;
};

void enqueue(struct queue_t *queue, uint32_t value)
{
    if (queue->ptr   1 >= QUEUE_LEN)
    {
        fprintf(stderr, "The queue is full");
        exit(1);
    }

    queue->data[queue->ptr  ] = value;
}

uint32_t dequeue(struct queue_t *queue)
{
    if (queue->ptr == 0)
    {
        fprintf(stderr, "Cannot dequeue empty queue");
        exit(1);
    }
    uint32_t val = queue->data[0];

    for (size_t i = 1; i ptr;   i)
    {
        queue->data[i - 1] = queue->data[i];
    }
    queue->ptr--;
    return val;
}

uint32_t peek(struct queue_t *queue)
{
    if (queue->ptr == 0)
    {
        fprintf(stderr, "Cannot peek empty queue");
        exit(1);
    }
    return queue->data[0];
}

Здесь есть интересная деталь реализации: всякий раз, когда мы удаляем из очереди, поскольку мы удаляем элемент из начала очереди,
мы должны переместить все следующие элементы назад, поэтому в этой реализации очередь имеет сложность O(n), чтобы избежать этого, нам нужно будет иметь LinkedList в качестве базовой структуры данных, сделав это, мы могли бы просто переместить указатель заголовка на следующий, вместо того, чтобы делать все это.

Лучшая реализация

#include 
#include 
#include 

struct node_t {
    uint32_t data;
    struct node_t *next;
};

struct linked_list_t {
    struct node_t *head;
    struct node_t *tail;
    size_t len;
};

void enqueue(struct linked_list_t *list, uint32_t data)
{
    struct node_t *node = malloc(sizeof(struct node_t));

    node->data = data;
    node->next = NULL;

    list->len  ;

    if (list->len == 1)
    {
        list->head = list->tail = node;
        return;
    }

    list->tail->next = node;
    list->tail = node;
}

uint32_t dequeue(struct linked_list_t *list)
{
    if (list->len == 0)
    {
        fprintf(stderr, "Cannot dequeue empty list");
        exit(1);
    }

    struct node_t *aux = list->head;
    uint32_t data = aux->data;

    list->head = list->head->next;
    list->len--;
    free(aux);

    return data;
}

uint32_t peek(struct linked_list_t *list)
{
    if (list->len == 0)
    {
        fprintf(stderr, "Cannot peek empty list");
        exit(1);
    }

    return list->head->data;
}

void list_free(struct linked_list_t *list)
{
    struct node_t *prev = NULL;
    struct node_t *aux = list->head;
    while (aux != NULL)
    {
        prev = aux;
        aux = aux->next;
        if (prev) {
            free(prev);
        }
    }
}

Здесь вы можете видеть, что при постановке в очередь и удалении из очереди не происходит никаких итераций, мы просто корректируем указатели, поэтому эта реализация имеет лучшую временную сложность при удалении из очереди.
Однако есть небольшое предостережение: благодаря локальности кэша, хотя эта реализация в худшем случае быстрее, в большинстве из них, вероятно, это не так.