Поскольку мы говорили о различных алгоритмах сортировки, сегодня мы изучим алгоритм сортировки выбором. Алгоритм сортировки, который учитывает возможное минимальное количество операций подкачки в среде с ограниченной памятью.

Оглавление

1. Введение
2. Что такое алгоритм сортировки выбором?
3. Как работает сортировка выбором?
   • Временная сложность
   • Космическая сложность
4. Реализация на JavaScript
5. Решение проблем с LeetCode
6. Заключение

Введение

Сортировка выбором — это простой, но эффективный алгоритм сортировки, который работает путем многократного выбора наименьшего (или самого большого) элемента из неотсортированной части списка и перемещения его в начало (или конец) отсортированной части. Этот процесс повторяется до тех пор, пока весь список не будет отсортирован. В этой статье мы углубимся в детали алгоритма сортировки выбором, его реализацию в JavaScript и его применение для решения реальных задач.

Что такое алгоритм сортировки выбором?

Алгоритм сортировки выбором — это алгоритм сортировки сравнением на месте. Он делит входной список на две части:

1. Отсортированная часть слева
2. Несортированная часть справа

Алгоритм неоднократно выбирает наименьший элемент из неотсортированной части и заменяет его самым левым несортированным элементом, перемещая границу между отсортированной и неотсортированной частями на один элемент вправо.

Как работает сортировка выбором?

Давайте рассмотрим пример с использованием массива [64, 25, 12, 22, 11]:

1. Начальный массив: [64, 25, 12, 22, 11]

• Отсортированная часть: []
• Несортированная часть: [64, 25, 12, 22, 11]

1. Первый проход:

• Найти минимум в неотсортированной части: 11
• Поменять местами 11 с первым неотсортированным элементом (64)
• Результат: [11, 25, 12, 22, 64]
• Отсортированная часть: [11]
• Несортированная часть: [25, 12, 22, 64]

1. Второй проход:

• Найти минимум в неотсортированной части: 12
• Поменять местами 12 на первый неотсортированный элемент (25)
• Результат: [11, 12, 25, 22, 64]
• Отсортированная часть: [11, 12]
• Несортированная часть: [25, 22, 64]

1. Третий проход:

• Найти минимум в неотсортированной части: 22
• Поменять местами 22 на первый неотсортированный элемент (25)
• Результат: [11, 12, 22, 25, 64]
• Отсортированная часть: [11, 12, 22]
• Несортированная часть: [25, 64]

1. Четвертый проход:

• Найти минимум в неотсортированной части: 25
• 25 уже в правильном положении
• Результат: [11, 12, 22, 25, 64]
• Отсортированная часть: [11, 12, 22, 25]
• Несортированная часть: [64]

1. Финальный проход:
   • Остался только один элемент, он автоматически оказывается в правильном положении
   • Конечный результат: [11, 12, 22, 25, 64]

Теперь массив полностью отсортирован.

Временная сложность

Сортировка выбором имеет временную сложность O(n^2) во всех случаях (наилучший, средний и худший), где n — количество элементов в массиве. Это потому что:

• Внешний цикл выполняется n-1 раз
• Для каждой итерации внешнего цикла внутренний цикл выполняется n-i-1 раз (где i — текущая итерация внешнего цикла)

Это приводит к примерно (n^2)/2 сравнениям и n заменам, что упрощается до O(n^2).

Из-за квадратичной временной сложности сортировка выбором неэффективна для больших наборов данных. Однако его простота и тот факт, что он выполняет минимально возможное количество свопов, могут сделать его полезным в определенных ситуациях, особенно когда вспомогательная память ограничена.

Космическая сложность

Сортировка выбором имеет пространственную сложность O(1), поскольку она сортирует массив на месте. Для этого требуется только постоянный объем дополнительной памяти независимо от размера входных данных. Это делает его более эффективным с точки зрения использования памяти, что может быть полезно в средах с ограниченной памятью.

Реализация в JavaScript

Вот реализация алгоритма сортировки выбором на языке JavaScript:

function selectionSort(arr) {
  const n = arr.length;

  for (let i = 0; i 


Давайте разберем код:

Мы определяем функцию selectSort, которая принимает на вход массив.
Мы перебираем массив с помощью внешнего цикла (i), который представляет границу между отсортированной и неотсортированной частями.
Для каждой итерации мы предполагаем, что первый неотсортированный элемент является минимальным, и сохраняем его индекс.
Затем мы используем внутренний цикл (j), чтобы найти фактический минимальный элемент в неотсортированной части.
Если мы находим элемент меньшего размера, мы обновляем minIndex.
После нахождения минимума при необходимости мы меняем его местами с первым неотсортированным элементом.
Мы повторяем этот процесс, пока весь массив не будет отсортирован.

  
  
  Решение проблем с LeetCode


Давайте решим одну задачу по алгоритму лит-кода, используя алгоритм сортировки выбором. А не ___ ли нам?

  
  
  Задача: сортировка массива [средний]


Задача: Дан массив целых чисел, отсортируйте его по возрастанию и верните его. Вы должны решить задачу без использования каких-либо встроенных функций с временной сложностью O(nlog(n)) и с минимально возможной пространственной сложностью.

Подход:: Чтобы решить эту проблему, мы можем напрямую применить алгоритм сортировки выбором. Это включает в себя перебор массива, поиск наименьшего элемента в неотсортированной части и замену его первым неотсортированным элементом. Мы повторяем этот процесс, пока весь массив не будет отсортирован.

Решение:

// This function sorts an array of integers in ascending order using the Selection Sort algorithm.
const sortArray = function (nums) {
  // Get the length of the input array.
  const n = nums.length;

  // Iterate through the array, starting from the first element.
  for (let i = 0; i 


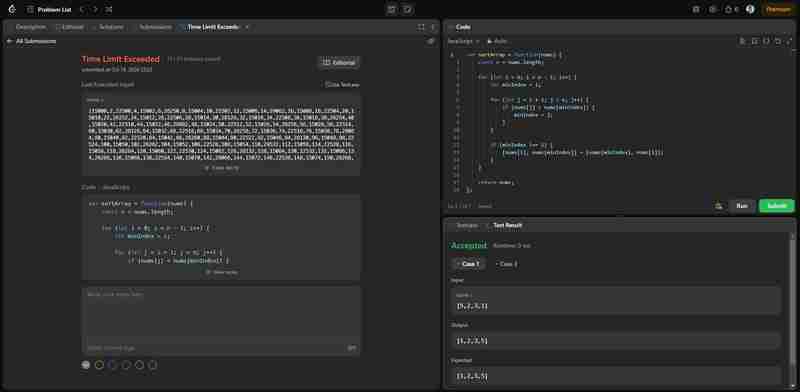
Это решение напрямую применяет алгоритм сортировки выбором, который мы реализовали ранее. Хотя оно правильно решает проблему, стоит отметить, что это решение может превысить ограничение по времени для больших входных данных в LeetCode из-за временной сложности O(n^2) сортировки выбором. На изображении ниже показано, что решение правильное, но неэффективное.



  
  
  Заключение


В заключение отметим, что сортировка выбором — это простой и интуитивно понятный алгоритм сортировки, который служит отличным введением в мир методов сортировки. Его простота облегчает понимание и реализацию, что делает его ценным инструментом обучения для начинающих. Однако из-за квадратичной временной сложности O(n^2) он неэффективен для больших наборов данных. Для больших наборов данных или приложений, критичных к производительности, предпочтительны более эффективные алгоритмы, такие как QuickSort, MergeSort или встроенные функции сортировки.


  
  
  Оставайтесь в курсе и на связи


Чтобы вы не пропустили ни одной части этой серии, а также связаться со мной для получения более подробной информации

дискуссии о разработке программного обеспечения (веб, сервер, мобильное устройство или парсинг/автоматизация), данных

структуры и алгоритмы, а также другие интересные технические темы, подписывайтесь на меня:



    
      

        
    
  

    

Великое решение ?Следуйте

    

      Инженер-программист | Технический писатель | Бэкэнд, веб- и мобильный разработчик? | Увлечен созданием эффективных и масштабируемых программных решений. #давайтеподключимся?
    
  

• GitHub
• LinkedIn
• X (Твиттер)

Следите за обновлениями и удачи в программировании ?‍??