JavaScript часто высмеивают, когда разработчики впервые сталкиваются с этим, казалось бы, сбивающим с толку результатом:

0.1   0.2 == 0.30000000000000004

Мемы об обработке чисел в JavaScript широко распространены, часто заставляя многих думать, что такое поведение уникально для этого языка.

Однако эта особенность не ограничивается только JavaScript. Это следствие того, как большинство языков программирования обрабатывают арифметику с плавающей запятой.

Например, вот фрагменты кода из Java и Go, которые дают схожие результаты:

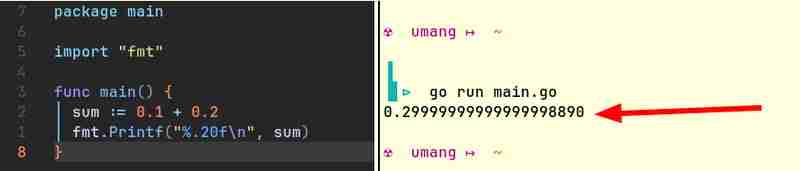
Компьютеры изначально могут хранить только целые числа. Они не понимают дроби. (Как они будут? Единственный способ, которым компьютеры могут выполнять арифметические действия, — это включать или выключать некоторые индикаторы. Индикатор может быть либо включен, либо выключен. Он не может быть включен «наполовину»!) Им нужен какой-то способ представления чисел с плавающей запятой. . Поскольку это представление не совсем точно, чаще всего 0,1 0,2 не равно 0,3.

Все дроби, знаменатели которых состоят из простых делителей основания системы счисления, могут быть четко выражены, в то время как любые другие дроби будут иметь повторяющиеся десятичные дроби. Например, в системе счисления с основанием 10 такие дроби, как 1/2, 1/4, 1/5, 1/10, представлены четко, поскольку знаменатели в каждом случае состоят из 2 или 5 – простых делителей 10. Однако такие дроби, как 1/3, 1/6, 1/7, имеют повторяющиеся десятичные знаки.

Аналогично, в двоичной системе дроби, такие как 1/2, 1/4, 1/8, выражаются четко, в то время как все остальные дроби имеют повторяющиеся десятичные дроби. Когда вы выполняете арифметические действия с этими повторяющимися десятичными знаками, вы получаете остатки, которые переносятся при преобразовании двоичного представления чисел компьютера в удобочитаемое представление по основанию 10. Именно это приводит к примерно правильным результатам.

Теперь, когда мы установили, что эта проблема характерна не только для JavaScript, давайте рассмотрим, как числа с плавающей запятой представляются и обрабатываются «под капотом», чтобы понять, почему происходит такое поведение.

Чтобы понять, как числа с плавающей запятой представляются и обрабатываются «под капотом», нам сначала нужно понять стандарт IEEE 754 с плавающей запятой.

Стандарт IEEE 754 — это широко используемая спецификация для представления и выполнения арифметических операций над числами с плавающей запятой в компьютерных системах. Он был создан, чтобы гарантировать согласованность при использовании арифметики с плавающей запятой на различных вычислительных платформах. Большинство языков программирования и аппаратных реализаций (ЦП, графические процессоры и т. д.) соответствуют этому стандарту.

Вот как число обозначается в формате IEEE 754:

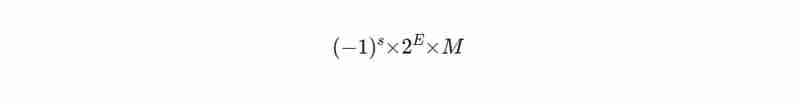
Здесь s — знаковый бит (0 для положительного значения, 1 для отрицательного), M — мантисса (содержит цифры числа) и E — показатель степени, определяющий масштаб числа.

Вы не сможете найти целочисленные значения для M и E, которые могли бы точно представлять такие числа, как 0,1, 0,2 или 0,3 в этом формате. Мы можем выбрать только те значения для M и E, которые дают наиболее близкий результат.

Вот инструмент, который можно использовать для определения обозначений десятичных чисел IEEE 754: https://www.h-schmidt.net/FloatConverter/IEEE754.html

нотация IEEE 754 0,25:

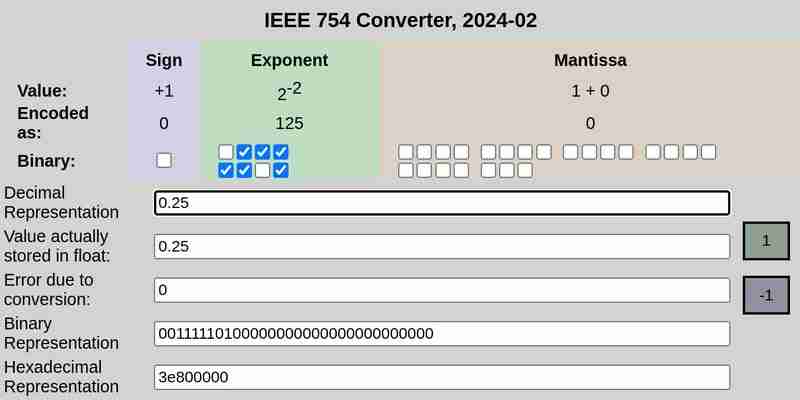
нотация IEEE 754 0,1 и 0,2 соответственно:

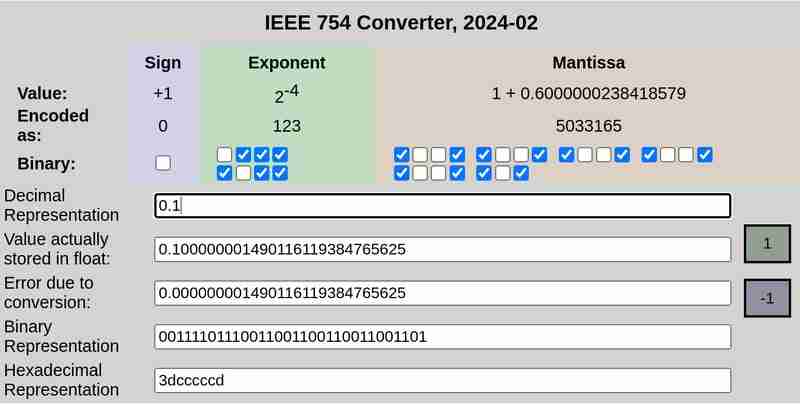
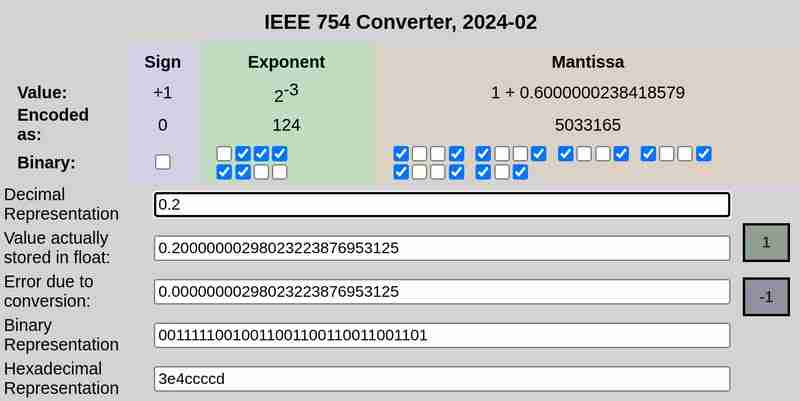
Обратите внимание, что ошибка преобразования в случае 0,25 была равна 0, а 0,1 и 0,2 имели ненулевые ошибки.

IEEE 754 определяет следующие форматы представления чисел с плавающей запятой:

• Одинарная точность (32 бита): 1 бит для знака, 8 бит для экспоненты, 23 бита для мантиссы

• Двойная точность (64 бита): 1 бит для знака, 11 бит для экспоненты, 52 бита для мантиссы

Для простоты давайте рассмотрим формат одинарной точности, который использует 32 бита.

32-битное представление 0,1:

0 01111011 10011001100110011001101

Здесь первый бит представляет знак (0, что в данном случае означает положительное значение), следующие 8 бит (01111011) представляют показатель степени, а последние 23 бита (10011001100110011001101) представляют собой мантиссу.

Это не точное представление. Он представляет собой ≈ 0,100000001490116119384765625

Аналогично, 32-битное представление 0,2:

0 01111100 10011001100110011001101

Это также не точное представление. Он представляет собой ≈ 0,20000000298023223876953125

При добавлении получается:

0 01111101 11001101010011001100110 

что равно ≈ 0,30000001192092896 в десятичном представлении.

В заключение, кажущийся озадачивающим результат 0,1 0,2 не дает 0,3 не является аномалией, специфичной для JavaScript, а является следствием ограничений арифметики с плавающей запятой во всех языках программирования. Корни такого поведения лежат в двоичном представлении чисел, что по своей сути приводит к ошибкам точности при обработке определенных дробей.