Удаление элемента из дерева AVL аналогично его удалению из BST, за исключением того, что может потребоваться перебалансировка дерева. Как обсуждалось в разделе «Удаление элементов из BST», для удаления элемента из двоичного дерева алгоритм сначала находит узел, содержащий этот элемент. Пусть current указывает на узел, содержащий элемент в двоичном дереве, а parent указывает на родительский узел current узла. Узел текущий может быть левым или правым дочерним элементом родительского узла.
При удалении элемента возникают два случая.

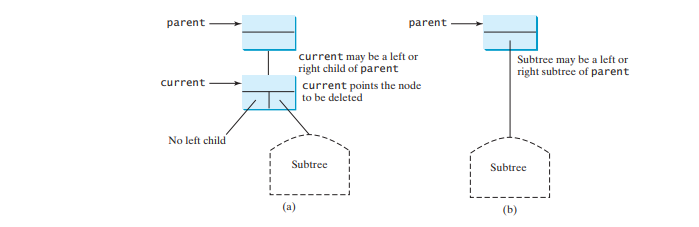
Случай 1: Узел текущий не имеет левого дочернего узла, как показано на рисунке ниже (a). Чтобы удалить узел current, просто соедините узел parent с правым дочерним элементом узла current, как показано на рисунке ниже (b). Высота узлов на пути от родительского узла до корня могла уменьшиться. Чтобы убедиться, что дерево сбалансировано, вызовите

balancePath(parent.element);

Случай 2: Узел текущий имеет левого дочернего элемента. Пусть rightMost указывает на узел, который содержит самый большой элемент в левом поддереве current узла, а parentOfRightMost указывает на родительский узел rightMost Узел , как показано на рисунке ниже (a). Узел rightMost не может иметь правого дочернего узла, но может иметь левого дочернего элемента. Замените значение элемента в узле current на значение в узле rightMost, соедините узел parentOfRightMost с левым дочерним элементом узла rightMost и удалите узел rightMost, как показано на рисунке ниже (b).

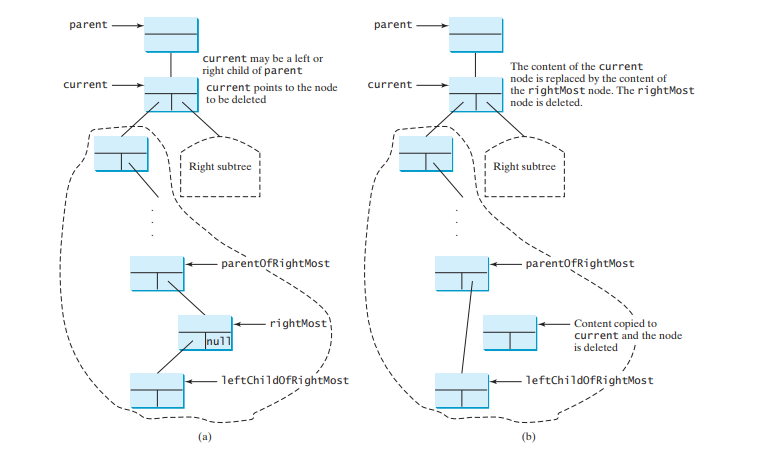
Возможно, уменьшилась высота узлов на пути от parentOfRightMost до корня. Чтобы убедиться, что дерево сбалансировано, вызовите

balancePath(parentOfRightMost);