В этом разделе представлены эффективные алгоритмы поиска ближайшей пары точек с использованием метода «разделяй и властвуй». Учитывая набор точек, задача ближайшей пары состоит в том, чтобы найти две точки, ближайшие друг к другу. Как показано на рисунке ниже, рисуется линия, соединяющая две ближайшие точки в анимации ближайшей пары.

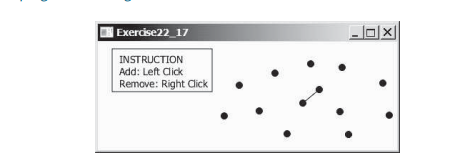
Пример: поиск ближайшей пары: представлен алгоритм грубой силы для поиска ближайшей пары точек. Алгоритм вычисляет расстояния между всеми парами точек и находит точку с минимальным расстоянием. Очевидно, что алгоритм занимает время O(n^2). Можем ли мы разработать более эффективный алгоритм?

Для решения этой проблемы мы воспользуемся подходом под названием разделяй и властвуй. Этот подход делит проблему на подзадачи, решает подзадачи, а затем объединяет решения подзадач для получения решения всей проблемы. В отличие от подхода динамического программирования, подзадачи подхода «разделяй и властвуй» не пересекаются. Подзадача аналогична исходной задаче, но имеет меньший размер, поэтому для ее решения можно применить рекурсию. Фактически, все решения рекурсивных задач основаны на подходе «разделяй и властвуй».

Приведенные ниже шаги описывают, как решить задачу о ближайшей паре, используя подход «разделяй и властвуй».

• Шаг 1: Отсортируйте точки в порядке возрастания координат x. Для точек с одинаковыми координатами X выполните сортировку по координатам Y. В результате получается отсортированный список S точек.
• Шаг 2. Разделите S на два подмножества, S1 и S2, одинакового размера, используя среднюю точку в отсортированном списке. Пусть середина находится в S1. Рекурсивно найдите ближайшую пару в S1 и S2. Пусть d1 и d2 обозначают расстояние до ближайших пар в двух подмножествах соответственно.
• Шаг 3: Найдите ближайшую пару между точкой в ​​S1 и точкой в ​​S2 и обозначьте их расстояние как d3. Ближайшей парой является та, которая находится на расстоянии min(d1, d2, d3).

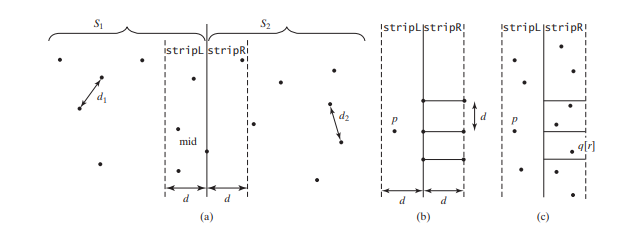
Сортировка выбором занимает время O(n^2). Шаг 1 можно выполнить за время O(n log n). Шаг 3 можно выполнить за время O(n). Пусть d = min(d1, d2). Мы уже знаем, что ближайшее парное расстояние не может быть больше d. Чтобы точка в S1 и точка в S2 образовали ближайшую пару в S, левая точка должна находиться в stripL, а правая точка — в stripR, как показано на рисунке ниже ( а).

Для точки p в stripL вам нужно рассмотреть только правую точку внутри прямоугольника d X 2d, как показано ниже (b). Любая правая точка вне прямоугольника не может образовать ближайшую пару с p. Поскольку расстояние до ближайшей пары в S2 больше или равно d, может быть не более шести
точки в прямоугольнике. Таким образом, для каждой точки в stripL необходимо учитывать не более шести точек в stripR.

Для каждой точки p в stripL как расположить точки в соответствующей области прямоугольника d X 2d в stripR? Это можно сделать эффективно, если точки в stripL и stripR отсортировать в порядке возрастания их координат Y. Пусть pointsOrderedOnY — список точек, отсортированных в порядке возрастания координат y. pointsOrderedOnY можно получить заранее в алгоритме. stripL и stripR можно получить из pointsOrderedOnY на шаге 3, как показано в коде ниже.

для каждой точки p в PointsOrderedOnY
если (p находится в S1 и middle.x – p.x добавить p к StripL;
иначе, если (p находится в S2 и p.x - middle.x добавить p к StripR;

Пусть точки в stripL и stripR будут {p0, p1, ... , pk} и {q0, q1, ... , qt}, как показано на рисунке Рисунок выше (в). Ближайшую пару между точкой в ​​stripL и точкой в ​​stripR можно найти с помощью алгоритма, описанного в коде ниже.

d = min(d1, d2);
 r = 0; // r is the index of a point in stripR
 for (each point p in stripL) {
 // Skip the points in stripR below p.y - d
  while (r 



Точки в stripL рассматриваются от p0, p1, ... , pk в указанном порядке. Для точки p в stripL пропустите точки в stripR, которые находятся ниже p.y – d (строки 5–6). Если балл пропущен, он больше не будет учитываться. Цикл  while (строки 9–17) проверяет, является ли (p, q[r1]) возможной ближайшей парой. Таких пар q[r1] не более шести, поскольку расстояние между двумя точками в stripR не может быть меньше, чем d. Таким образом, сложность поиска ближайшей пары на шаге 3 равна O(n).

Обратите внимание, что шаг 1 в приведенных выше шагах выполняется только один раз для предварительной сортировки точек. Предположим, что все точки предварительно отсортированы. Пусть T(n) обозначает временную сложность этого алгоритма. Таким образом,



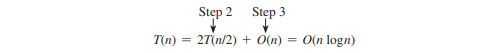
Следовательно, ближайшую пару точек можно найти за время O(n log n).